SOLUTION: Hi there. I need help with these questions. Writing each first in vertex form, and then in standard form. 1) vertex (3,5) and passing through (1,1) 2) vertex (1,-7) and passing

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Hi there. I need help with these questions. Writing each first in vertex form, and then in standard form. 1) vertex (3,5) and passing through (1,1) 2) vertex (1,-7) and passing      Log On


   

Question 887457: Hi there. I need help with these questions. Writing each first in vertex form, and then in standard form.
1) vertex (3,5) and passing through (1,1)
2) vertex (1,-7) and passing through (-2,29)
3) vertex (-6,-5) and passing through (-3,4)
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!
Vertex form and standard form are the same thing.

The basic idea is to use the given data and use y=a%28x-h%29%5E2%2Bk for the vertex (h,k). The point being "passed through" helps to get the value of a.

You do like this:
Vertex (h,k) passing through (u,v).
highlight_green%28y=a%28x-h%29%5E2%2Bk%29, and you want to find a.
a%28x-h%29%5E2=y-k
a=%28y-k%29%2F%28x-h%29%5E2
Substitute the given point
highlight_green%28a=%28v-k%29%2F%28u-h%29%5E2%29, and compute if using unvaried given numbers for v,u, k and h.
Finish writing the equation with the found and now known values for a, h, and k.

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

Hi there. I need help with these questions. Writing each first in vertex form, and then in standard form.
1) vertex (3,5) and passing through (1,1)
2) vertex (1,-7) and passing through (-2,29)
3) vertex (-6,-5) and passing through (-3,4) 


Doing 1 of the 3 should be enough for you to follow

Vertex, or (h, k) = (3, 5), and pass-through point, (x, y) being (1, 1)

Vertex equation-form of a parabola: y+=+a%28x+-+h%29%5E2+%2B+k becomes:

1+=+a%281+-+3%29%5E2+%2B+5 ----- Substituting variables to determine the value of "a"

1+=+a%28-+2%29%5E2+%2B+5

1 = 4a + 5

4a = 1 - 5

4a = - 4

a+=+%28-+4%29%2F4, or - 1



Vertex form:   highlight_green%28highlight_green%28y+=+-+%28x+-+3%29%5E2+%2B+5%29%29

y+=+-+%28x+-+3%29%5E2+%2B+5

y+=+-+%28x%5E2+-+6x+%2B+9%29+%2B+5

y+=+-+x%5E2+%2B+6x+-+9+%2B+5

Standard form: 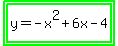highlight_green%28highlight_green%28y+=+-+x%5E2+%2B+6x+-+4%29%29