Question 887128: I. Given the following polynomial: 2x^2+7x-15=0 . Check all that apply.
The value of the discriminant is 169.
There are 2 real roots.
There are 2 irrational roots.
The graph intersects the y-axis twice.
The parabola is directed upward.
The axis of symmetry is located at x=-7/4
The vertex is located at: (-7/4, -49/8)
The roots are: (5,3/2)
The graph intersects the y axis at (0, -15).
The graph intersects the x-axis at (-5, 0) and (1.5, 0)
HELP PLEASE
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Many of the questions depend on the discriminant.

Discriminant is  . .
What do you understand about the discriminant for a quadratic expression?
Something about the discriminant indicates that your quadratic expression is factorable.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I. Given the following polynomial: 2x^2+7x-15=0 . Check all that apply.
The value of the discriminant is 169.
There are 2 real roots.
There are 2 irrational roots.
The graph intersects the y-axis twice.
The parabola is directed upward.
The axis of symmetry is located at x=-7/4
The vertex is located at: (-7/4, -49/8)
The roots are: (5,3/2)
The graph intersects the y axis at (0, -15).
The graph intersects the x-axis at (-5, 0) and (1.5, 0)
HELP PLEASE
 , or , or


The value of the discriminant is 169. Discriminant:  , or , or 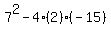 ___49 + 120 = 169 (CHECK) ___49 + 120 = 169 (CHECK)
There are 2 real roots. Since the value of DISCRIMINANT (169) > 0, then there are 2 REAL roots. (CHECK)
There are 2 irrational roots. Since the value of the DISCRIMINANT (169) is a perfect square ( ), roots ), roots
are RATIONAL (NO CHECK)
The graph intersects the y-axis twice. Substituting 0 for x in 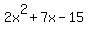 results in y being – 15. The results in y being – 15. The
graph has a sole y-intercept, at – 15 (NO CHECK)
The parabola is directed upward. Since a > 0, the parabola opens upwards. (CHECK)
The axis of symmetry is located at x = 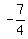 . Axis of symmetry is at . Axis of symmetry is at  , or , or  , or , or 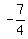 (CHECK) (CHECK)
The vertex is located at: (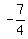 , , 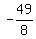 ). Substituting ). Substituting 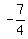 for x in for x in 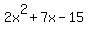 produces: produces: 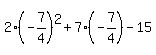 , ,
or  , or , or 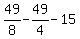 , or , or 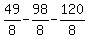 , or , or 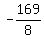 (NO CHECK) (NO CHECK)
The roots are: (5,3/2)____ factors to (2x - 3)(x + 5) = 0, so roots are: factors to (2x - 3)(x + 5) = 0, so roots are:  and and  (NO CHECK) (NO CHECK)
The graph intersects the y axis at (0, -15). The y-intercept was found to be – 15, so y-intercept is (0, - 15).
This is a CHECK.
The graph intersects the x-axis at (-5, 0) and (1.5, 0). As seen above, roots are 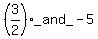 , so the graph , so the graph
intersects the x-axis at ( , ,  ) and ( ) and (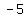 , ,  ). This is a CHECK. ). This is a CHECK.
|
|
|