If you have a polynomial equation of the form p(x) = 0,
When the degree of the polynomial is even, and the leading term's
coefficient is 1, the product of all its solutions is the constant
term.
When the degree of the polynomial is odd, and the leading term's
coefficient is 1, the product of all its solutions is the constant
term with the sign changed.
The degree of 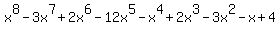

 is 8
8 is an even number, and its leading term's coefficient is 1, so
the product of its solutions is its constant term 4.
[If the leading coefficient is not 1, you can always make it 1 by
dividing every term by the leading coefficient.]
Edwin
is 8
8 is an even number, and its leading term's coefficient is 1, so
the product of its solutions is its constant term 4.
[If the leading coefficient is not 1, you can always make it 1 by
dividing every term by the leading coefficient.]
Edwin