SOLUTION: Find the inverse of F(x)= -√3x-4. Determine the domain of the original function. Determine whether the inverse is also a function, and find the domain and range of the

The other tutor did not give you the correct inverse, because the inverse
must have a restricted domain, which he ignored. He stated that the domain
of the inverse is "all real numbers", but that is wrong. It is necessary that
you think of how the graph of the function and its inverse must be.

Here is the graph of 



The dotted like is called the "Identity function" y=x.  The inverse
of a graph is the reflection of the graph in (or across) this dotted
line.  Here is the graph of the inverse, in blue, which is the  
reflection of the red graph in the dotted identity line (in green).



What the other tutor told you, namely this part:

  

is correct.  But you cannot stop there.  That's because the graph of

 is the blue graph below, which
extends too far to the left, and the part of that graph that extends
into the second quadrant (part of the blue graph left of the y-axis),
is NOT part of the inverse and it must be eliminated by restricting
the domain of the inverse. The other tutor's error was his failure to 
restrict the domain. He said 

which is wrong!!!!

   

Here is the corrected version:

Original function:

F(x)

Original function's domain: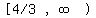 
Original function's range:    

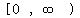Inverse function [when the original function if labeled F(x), the inverse
                  function must be labeled F-1(x).  The other
                  tutor just labeled it "y".  That's wrong. you must
                  change the "y" to F-1(x). 

F-1(x) <--notice the restriction!

Inverse function's domain: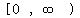   
Inverse function's range:  

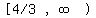Notice that the domain of the original function is the same as the
range of the inverse function, and the range of the original function
is the same as the domain of the inverse function.

Edwin