Question 885759: If. A(-8;6),B,C and D(3;9) are vertices of a rhombus. The equation for AC is 3y=-x+10
Show that BD is 3x-Y=0
2. Calculate. The co-ordinates of k the intersection of the diagonals of the rhombus ABCD
Found 2 solutions by richwmiller, Edwin McCravy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The green line is the line 3y=-x+10
As you can see from the graphs below, there are two possible
solutions for the rhombus.
  There is a mistake in your problem, for as you see the line BD cannot
possibly pass through the origin, yet the problem states:
"Show that BD is 3x-y=0"
But 3x-y=0 passes through the origin (0,0), so there is no way that
3x-y=0 could be the equation of BD.
Let's find what the equation of BD really is.
BD is parallel to AC and has the same slope.
AC has the equation
There is a mistake in your problem, for as you see the line BD cannot
possibly pass through the origin, yet the problem states:
"Show that BD is 3x-y=0"
But 3x-y=0 passes through the origin (0,0), so there is no way that
3x-y=0 could be the equation of BD.
Let's find what the equation of BD really is.
BD is parallel to AC and has the same slope.
AC has the equation    Solving for y,
Solving for y,    thus the slope of AC and BD is
thus the slope of AC and BD is  And BD passes through D(3,9)
Using the point-slope formula:
And BD passes through D(3,9)
Using the point-slope formula:
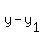  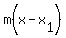
   Multiply through by 3
Multiply through by 3
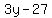  {{-{x-3)}}} {{-{x-3)}}}
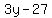  {{-x+3}}} {{-x+3}}}
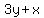   This is correct equation for BD, not 3y-x=0.
Now we must find the coordinates of the K, the intersection of the
diagonals. Since the diagonals of a parallellogram bisect each other,
we only need to find the midpoint of one of the diagonals. We will
need to find the coordinates of C, and then K will be the midpoint of
diagonal CD.
Since this is a rhombus, all sides must be equal. So we find side
AD using the distance formula:
This is correct equation for BD, not 3y-x=0.
Now we must find the coordinates of the K, the intersection of the
diagonals. Since the diagonals of a parallellogram bisect each other,
we only need to find the midpoint of one of the diagonals. We will
need to find the coordinates of C, and then K will be the midpoint of
diagonal CD.
Since this is a rhombus, all sides must be equal. So we find side
AD using the distance formula:
  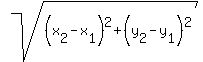
  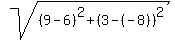
  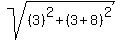
  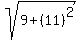
  
   So the length of all 4 sides is
So the length of all 4 sides is   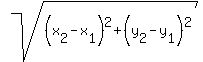
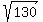  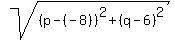
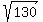  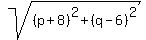 Square both sides:
Square both sides:
   Now we must solve this system of equations to find p and q,
the coordinates of C
Now we must solve this system of equations to find p and q,
the coordinates of C
 Solve the first equation for p, p = 10-3q
Substitute in the second equation,
Solve the first equation for p, p = 10-3q
Substitute in the second equation,
  
  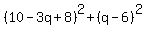
  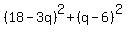
  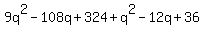
  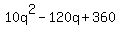
   Divide through by 10
Divide through by 10
  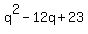 Solve by the quadratic formula and get
Solve by the quadratic formula and get
  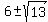 using the +, substitute in
using the +, substitute in
  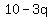
  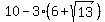
  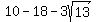
   So point C in the graph on the right above is
So point C in the graph on the right above is
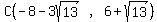 using the -, substitute in
using the -, substitute in
  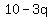
  
  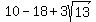
   So point C in the graph on the left above is
So point C in the graph on the left above is
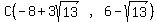 Now we will find the midpoint of CD which will be K,
where the two diagonals intersect.
We will find K for the graph on the left.
For the graph on the left
Now we will find the midpoint of CD which will be K,
where the two diagonals intersect.
We will find K for the graph on the left.
For the graph on the left
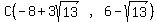 and D(3,9)
Using the midpoint formula:
Midpoint = and D(3,9)
Using the midpoint formula:
Midpoint = 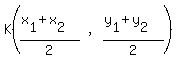 Midpoint =
Midpoint =  Midpoint =
Midpoint = 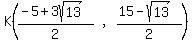 For the graph on the right
For the graph on the right
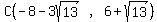 and D(3,9)
Using the midpoint formula:
Midpoint = and D(3,9)
Using the midpoint formula:
Midpoint = 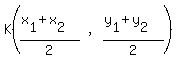 Midpoint =
Midpoint =  Midpoint =
Midpoint =  Edwin
Edwin
|
|
|