Question 885722: A plane goes 150 miles with the wind and returns against the wind in 3 hours and 45 minutes. Find the air speed of the plane if the wind blows 10 mph.
I tried to set it up as (150) / (s+10) + (150) / (s-10) = 3.75 but whenever I solve I don't get the right answer.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! RT=D for rate, time, distance.
10 mph = the speed of just the wind
Let r = the speed of the plane if no wind
DATA TABLE often helps to think clearly about all the values and numbers used in the problem description.
______________________speed_________time_________distance
WITH WIND_____________r+10__________(____)_______150
AGAINST Wind__________r-10_________(_____)_______150
TOTAL_______________________________3.75
You need expressions for times. RT=D means you can divide left and right members of such an equation by R, so you have T=D/R. Use this to fill the time slots in the table.
______________________speed_________time_________distance
WITH WIND_____________r+10__________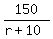 _______150 _______150
AGAINST Wind__________r-10_________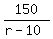 _______150 _______150
TOTAL_______________________________3.75
The time column including the total gives you an equation in the variable, r:
 . .
That is a large part of this solution process: That analysis and obtaining the outlined equation.
Solve the equation for r.
(I used r, while you used s. I hope you are not bothered by that.)
-
(Now I see you got the same equation as I did, but you could not get an answer you were comfortable with. Did you try multiplying left and right sides by (r+10)(r-10) and then simplify?)
Excuse me for skipping several steps; but you could get to
 , and since the mixed decimal involves a denominator of 4, you can multiply left and right members by 4, yielding , and since the mixed decimal involves a denominator of 4, you can multiply left and right members by 4, yielding
 and continue to simplify this and continue to simplify this
 ---- Now, solve THAT for r. ---- Now, solve THAT for r.
-
Use the general solution of a quadratic formula and simplify your expression. I found  . .
|
|
|