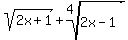

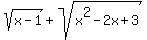 We wonder if each of the radical expressions on the left equals to one of
the radical expressions on the right.
We try the first expression on left equaling to the first
expression on the right
We wonder if each of the radical expressions on the left equals to one of
the radical expressions on the right.
We try the first expression on left equaling to the first
expression on the right



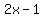




 We check to see if that makes the other radicals equal:
We check to see if that makes the other radicals equal:


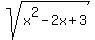
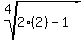


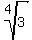

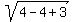
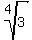

 No, those are not equal. So 2 is not a solution.
So we try the first expression on the
left equaling to the second expression on the right:
No, those are not equal. So 2 is not a solution.
So we try the first expression on the
left equaling to the second expression on the right:


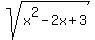


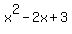


 We could solve this by the quadratic formula but there
would be no use unless also the second expression on the left
equals the first expression on the right. So we'll wait and
see if that can be the case:
To see if that can be the case, we set those equal:
We could solve this by the quadratic formula but there
would be no use unless also the second expression on the left
equals the first expression on the right. So we'll wait and
see if that can be the case:
To see if that can be the case, we set those equal:


 Square both sides. The square of a fourth root equals
the square root:
Square both sides. The square of a fourth root equals
the square root:


 Square both sides again:
Square both sides again:





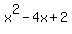 We're in luck! That just happens to be the same
quadratic, so we will solve it by the quadratic formula:
We're in luck! That just happens to be the same
quadratic, so we will solve it by the quadratic formula:


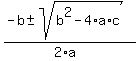


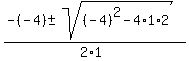








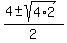


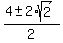


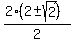


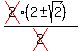


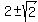 We must check solutions of equations containing radicals,
as they often have extraneous answers.
All the roots in the equation have even indices, so the
four radicands must not be negative.
We only need to make sure that there are no negative
numbers under any of the radicals:
The first radicand is
We must check solutions of equations containing radicals,
as they often have extraneous answers.
All the roots in the equation have even indices, so the
four radicands must not be negative.
We only need to make sure that there are no negative
numbers under any of the radicals:
The first radicand is
 Substituting
Substituting 

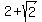
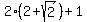 , that's positive. So far so good.
Substituting
, that's positive. So far so good.
Substituting 

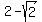
 , that's positive also. OK.
The second radicand is
, that's positive also. OK.
The second radicand is
 Substituting
Substituting 

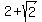
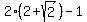 , that's positive
Substituting
, that's positive
Substituting 

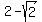
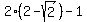 , that's positive also.
The third radicand is
, that's positive also.
The third radicand is
 Substituting
Substituting 

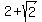
 , that's positive
Substituting
, that's positive
Substituting 

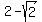
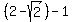
 Oh oh, that's negative, so
Oh oh, that's negative, so 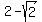 is an extraneous answer and must be discarded.
Thus the only solution possible is
is an extraneous answer and must be discarded.
Thus the only solution possible is  , but we
must make sure it gives a positive radicand in the last
expression on the right:
The fourth radicand is
, but we
must make sure it gives a positive radicand in the last
expression on the right:
The fourth radicand is
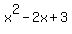 Substituting
Substituting 


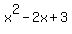
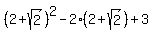
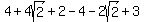
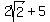 , that's positive.
So there is one solution:
, that's positive.
So there is one solution:


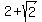 Edwin
Edwin