SOLUTION: How many 5-digit numbers contain at least one 3?

When you see "at least one" in a probability problem, you usually first
first find the probability of the complement event, which is "none at all",
and then subtract from 1.  That's what we do here.

First we find the denominator of the probability, which
is the number of 5 digit numbers:

There are two ways to determine this.

First way:  The number of 5-digit numbers is 99999 minus all
the numbers with fewer than 5 digits, which is 9999, So the
number of 5-digit numbers is 99999-9999 = 90000

Second way:
Choose the 1st digit 9 ways (can't choose 0).
Choose the 2nd digit 10 ways (can choose 0).
Choose the 3rd digit 10 ways.
Choose the 4th digit 10 ways.
Choose the 5th digit 10 ways.

9×10×10×10×10 = 90000

Now we find the numerator, which is all the 5-digit numbers
which do not contain a 3.  That is, we choose only digits from
these 9 {0,1,2,4,5,6,7,8,9}

Choose the 1st digit 8 ways (can't choose 0).
Choose the 2nd digit 9 ways (can choose 0).
Choose the 3rd digit 9 ways.
Choose the 4th digit 9 ways.
Choose the 5th digit 9 ways.

8×9×9×9×9 = 52488

Probability of complement event = 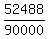 which
reduces to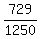 

Desired probability =  

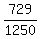
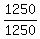
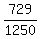
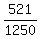Edwin