The mean television viewing time for teens is 3 hours per day. Assume = 3 and population standard deviation is = 1.2 hours. Suppose a sample of 50 teens will be used to monitor television viewing time. What is the probability the sample mean will be within 0.25 hours of the population mean?
We find the z-scores for 3-.25 = 2.25 and 3+.25 = 3.25
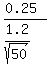
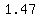Then looking up the area between z=-1.47 and 1.47 gives 0.8584.
So you're right on that part. But if you do it on a TI graphing
calculator, you get:
normalcdf(3-.25,3+.25,3,1.2/√(50))
0.8592864055 which is more accurate because the calculator carries
everything to a lot more decimal places than the normal table.
what is the probability the sample mean will be less than 2.7 hour?
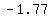So you want the area to the left of z = -1.77.
If your normal table has negative z-values, then you simply
find z=-1.77 in the table as the area (probability) 0.0384.
If your normal table does not have negative z-values you
look up 1.77 and find the area between z=0 and z=1.77 as 0.4616, then
subtract from 0.5000 to get the area to the right of 1.77, which is
0.0384. That's the answer because the area to the right of z=+1.77
by symmetry is the same as the area to the left of z=-.1.77
Either way, the answer is 0.0384 using either kind of 4-place
normal table.
However with a TI graphing calculator, you get:
normalcdf(-9999999999,2.7,3,1.2/√(50))
0.0385498886.
Edwin
