Question 885241: The doubling period of a baterial population is 15 minutes. At time t = 90 minutes, the baterial population was 50000. Round your answers to at least 1 decimal place.
What was the initial population at time t = 0 ?
Find the size of the baterial population after 4 hours
Found 2 solutions by ankor@dixie-net.com, KMST:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! The doubling period of a bacterial population is 15 minutes.
At time t = 90 minutes, the bacterial population was 50000.
Round your answers to at least 1 decimal place.
:
We can use the formula:
A = Ao*2^(t/d); where:
A = amt after t time
Ao = initial amt (t=0)
t = time period in question
d = doubling time of substance
In our problem
d = 15 min
t = 90 min
A = 50000
What was the initial population at time t = 0
Ao * 2^(90/15) = 50000
Ao * 2^6 = 50000
We know 2^6 = 64
64(Ao) = 50000
Ao = 50000/64
Ao = 781.25 is the initial population
:
Find the size of the bacterial population after 4 hours
Change 4 hr to 240 min
A = 781.25 * 2^(240/15
A = 781.25 * 2^16
A= 781.25 * 65536
A = 51,199,218.75 after 4 hrs
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! WITHOUT FORMULAS OR CALCULATOR (but with understanding):
The population of that kind of bacteria doubles every 15 minutes, and after 90 minutes there's 50,000 bacteria.
At time t=90 minutes,  doublings have happened since 
The population at t=90 minutes is  times the population at ,
so the population at t=0 must have been
I do not need to round that number, because it is an exact calculation.
Saying that at time t=0 there were 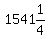 bacteria is a little silly.
I expect the number of bacteria to be an integer.
However, the problem asks to round to at least 1 decimal place, so let's be silly.
How did I calculate that result? With pencil and paper.
At t=4 hours,  doubling period have passed since t=0.
That is  doubling periods after t=90 minutes,
so the number of bacteria should be  times what it was at 90 minutes.
That is  and that is an exact number too.
Should I say it is 51,200,000.00 to have at least one decimal place expressly stated.
How did I calculate that result? With pencil and paper.
WITH FORMULAS AND CALCULATOR:
We are having a case of exponential growth.
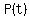 = population at t=t minutes
 <-->
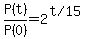
Since calculators allow us to calculate natural logarithms, and base 10 logarithms,
we can also write that as
 or 
Going from the natural logarithms version to exponentials on base  we get
 <--->
Those are very popular forms. The approximation  is often used.
At  ,
 --> --> -->-->
}}} (using the calculator's value for  )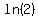
(Using 0.693 will give you a different decimal part).
At  ,
 --> -->
|
|
|
