Question 884963: Find the sum of all positive integers which are less than 2010 and are not divisible by 3
Found 2 solutions by Edwin McCravy, josmiceli:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
2010 is divisible by 3, so the largest integer less than 2010
that is divisible by 3 is 3 less that 2010, or 2007
First use the sum formula to find the sum of ALL integers less than
2010, which are the integers 1,2,3,...,2009
Sn =  (a1 + an)
with n=2009, a1 = 1, an = 2009, to find the sum of all
positive integers less than 2010, the integers 1,2,3,...,2009.
Now we need to find the sum of the integers which are divisible by 3.
They are these:
3,6,9,...,2007
We can find n, which is how many there are, by thinking of dividing
them all by 3 and getting
1,2,3,...669
So we know there are 669 multiples of 3 less than 2010. So we
use the sum formula again
Sn = (a1 + an)
with n=2009, a1 = 1, an = 2009, to find the sum of all
positive integers less than 2010, the integers 1,2,3,...,2009.
Now we need to find the sum of the integers which are divisible by 3.
They are these:
3,6,9,...,2007
We can find n, which is how many there are, by thinking of dividing
them all by 3 and getting
1,2,3,...669
So we know there are 669 multiples of 3 less than 2010. So we
use the sum formula again
Sn =  (a1 + an)
this time with n=669, a1 = 3, an = 2007
to find the sum of all integers divisible by 3 which are less
than 2010, which are 3,6,9,...,2007.
Then finally, to find the sum of all positive integers which are
less than 2010 and are not divisible by 3, we subtract the second
number from the first number.
Answer: 672345
Edwin (a1 + an)
this time with n=669, a1 = 3, an = 2007
to find the sum of all integers divisible by 3 which are less
than 2010, which are 3,6,9,...,2007.
Then finally, to find the sum of all positive integers which are
less than 2010 and are not divisible by 3, we subtract the second
number from the first number.
Answer: 672345
Edwin
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, I looked at the numbers starting with 3
that ARE divisible by 3:
3, 6, 9, 12, 15, . . .
----------------------
I noticed that:
3 = 1 + 2
6 = 2 + 4
9 = 3 + 6
12 = 4 + 8
. . .
-------------
And then:
3 = 1 + 1 + 1
6 = 2 + 2 + 2
9 = 3 + 3 + 3
12 = 4 + 4 + 4
. . .
----------------
How MANY numbers less than 2010
are divisible by 3?
That would be 
------------------------------------------
I know how to find the sum 1 + 2 + 3 + 4 + 5 + . . . + n
It is 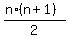
In the case of  , it is: , it is:

---------------------------
So, it looks like I need to find
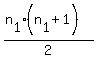 where where 
Then I need to subtract:
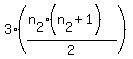 where where 
----------------------------------------------



I get 1,406,910 for the sum
---------------------------
Maybe there is an easier way to do this, though
================================
Checking it for less than 1 through 20, you have
1 + 2 + 4 + 5 + 7 + 8 + 10 + 11 + 13 + 14 + 16 + 17 + 19
 total total
----------------
Using the formula:
 ( nearest whole number ) ( nearest whole number )
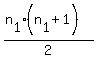

and
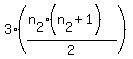


seems to work
|
|
|