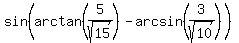 Let
Let 

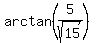 and
and 

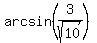
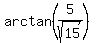 means the angle whose tangent is
means the angle whose tangent is 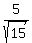 .
The tangent is
.
The tangent is 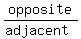 so let's draw a right triangle
containing angle
so let's draw a right triangle
containing angle  by using the numerator of
by using the numerator of 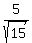 , which
is 5, for the opposite side, and using the denominator of
, which
is 5, for the opposite side, and using the denominator of 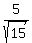 ,
which is
,
which is 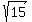 for the opposite side.
for the opposite side.
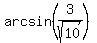 means the angle whose sine is
means the angle whose sine is  .
The sine is
.
The sine is 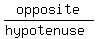 so let's draw another right triangle
containing angle
so let's draw another right triangle
containing angle  by using the numerator of
by using the numerator of  , which is
3, for the opposite side, and using the denominator of
, which is
3, for the opposite side, and using the denominator of  , which
is
, which
is  for the hypotenuse.
for the hypotenuse.

 We calculate the hypotenuse of the first right triangle and
the adjacent side to
We calculate the hypotenuse of the first right triangle and
the adjacent side to  in the second one:
in the second one:












 Put those values on the triangles:
Put those values on the triangles:

 Now
Now
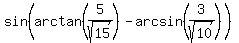

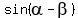

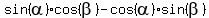

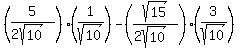

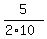

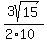

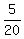

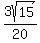

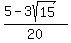 Edwin
Edwin