Question 883651: Find the slope of the line bisecting the angle from line1, with slope 2, to line2, with no slope.
Hope you'll help me. Thanks! Will wait asap.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are only given slopes, so it must mean that y-intercepts do not matter.
The lines could intersect each other anywhere, and they could intersect the x- and y-axes anywhere,
but for convenience I will make the lines intersect at the origin.
(Whoever does not like my drawing can move the axes up, down, and left or right to his/her taste. As long as nothing is rotated, the slopes remain the same).
 The slope of line 1 is the tangent of the angle The slope of line 1 is the tangent of the angle 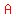 it makes with the x-axis (measured counterclockwise from the positive x-axis). it makes with the x-axis (measured counterclockwise from the positive x-axis).
The slope of the y-axis is undefined, and line 2 is the y-axis.
The bisector of the acute angle formed by lines 1 and 2 is drawn in green.
The angle it forms with the positive x-axis is
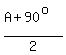
(If you don't like degrees, it is 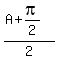 in radians). in radians).
The slope of the bisector is the tangent of that angle.
If you only need an approximate value, you could use inverse trigonometric functions.
For an exact value, I would use trigonometric identities.
USING INVERSE FUNCTIONS:
We use the inverse of tangent from calculator or computer to find the angle that has a tangent of  . .
Hopefully you know how to do that with your calculator and/or computer.
The inverse function of tangent is represented as  , or , or 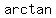 , or , or  , and in some calculators you have to press a key for inverse functions and then the tangent key. , and in some calculators you have to press a key for inverse functions and then the tangent key.
 ---> ---> (rounded), (rounded),
or  (rounded) in radians, if you prefer radians. (rounded) in radians, if you prefer radians.
Using  : :
 and and  (rounded) is the approximate value for the slope of the bisector. (rounded) is the approximate value for the slope of the bisector.
Using  (in radians): (in radians):
 (rounding the result but not (rounding the result but not 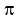 ), and ), and
 (rounded) is the approximate value for the slope of the bisector. (rounded) is the approximate value for the slope of the bisector.
You could round to more digits to get a better approximation.
USING TRIGONOMETRIC IDENTITIES FOR EXACT VALUE:
From the values of the trigonometric functions for 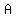 , ,
and the well known values for  , ,
we would like to find the trigonometric functions for  . .
For easier typing, I am going to use 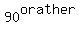 from now on. from now on.
There are probably many ways to get to  , ,
but I am going to show the one that came to my mind first,
and that requires starting from  and and  . .
The right triangle with angle 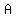 that I included in my sketch that I included in my sketch
has legs measuring  and and  , ,
so the Pythagorean theorem says that the length of the hypotenuse is  . .
Trigonometric ratios tell us that
 and and 
Trigonometric identities for sum of angles tell us that

We are half of he way there
Trigonometric identities for half angles are
 and and  , ,
and we have to figure out the sign for ourselves.
Since 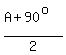 is in the first quadrant, we know that all its trigonometric functions have positive values, so is in the first quadrant, we know that all its trigonometric functions have positive values, so


Tangent is sine divided by cosine, so
 = = = =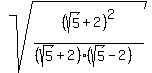 = =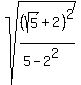 = =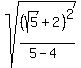 = =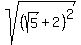 = =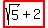
The approximate value of 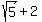 is is  . .
|
|
|