|
Question 883627: Find a positive integer for which the sum
of its recipricol and four times its square is the smallest
possible.
Found 2 solutions by stanbon, josgarithmetic:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Find a positive integer for which the sum
of its recipricol and four times its square is the smallest
possible.
---------
S = 1/x + 4x^2
------
Take the derivative to get:
S' = -1/x^2 + 8x
------
Solve:: -1/x^2 + 8x = 0
8x^3 = 1
x = 1/2
================
Cheers,
Stan H.
================
Answer by josgarithmetic(39620) (Show Source):
You can put this solution on YOUR website! Integer to find, n. Is this for a Calculus course, or College Algebra/Intermediate Algebra?
 and you want y as small as possible; and n must be an integer. Use derivative, 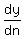 . This should be 0 at any extreme value for y, including any minimum.
-
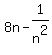
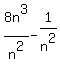
Finding extreme values for y
 ignoring the denominator because it has no importance for equating the derivative to zero.
Based on the difference of cubes formula,  .
This would have three possible solutions for n, but maybe only one of them would be our minimum n for y.
The binomial:
The quadratic:
Discriminant,  , not a real number.
Only that one, real, extreme value so must be our input for the minimum for y.
We want an INTEGER, so the nearest ones to  are 0 and 1.
-
In fact for smallest POSITIVE value for y, choose n=1.
|
|
|
| |
