Question 883310: Please help me on this. This is confusing (it's solution) 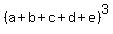 Thanks In Advance Thanks In Advance
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAIMERS:
I am not sure what the question is (what is expected).
Maybe there is a more elegant solution.
MY BEST TRY:
To calculate 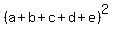 or or 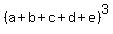 you can clench your teeth and start applying the distributive property, you can clench your teeth and start applying the distributive property,
or you can think of what multiplication means and try to figure out what the terms of the product should be.
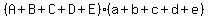
The product will have terms that represent all the possible products you could get multiplying one term of 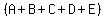 times one term of times one term of 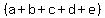 . .
There are many possibilities.
It is a question of combinations.
It is like choosing one drink from a 5-item list, and one food from a 5-item menu.
It is like choosing one of 5 available shorts, and one of 5 available T-shirts.
For 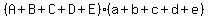 , you get , you get  different products. different products.
Five of the products are same letter products:
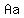 , ,  , ,  , , 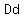 and and 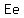 . .
The other 20 products are possible combinations of 2 different letters.
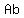 and and 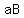 are 2 of them. are 2 of them.
(I like to write the factors in alphabetical order, but  ). ).
There are  ways of making those combinations of 2 different letters, ways of making those combinations of 2 different letters,
pairing each of the 5 capital letters with one of the 4 different lowercase letters.
When the two factors are the same,
as in  , ,
the 20 products with 2 different letters come in matching pairs,
because 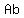 and and 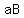 both turn into both turn into 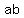 . .
You get 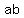 twice, and the same goes for all possible combinations of 2 different letters. twice, and the same goes for all possible combinations of 2 different letters.

Writing  is more efficient than writing each 2-letter product twice. is more efficient than writing each 2-letter product twice.
For  , ,
with 5 terms in each of the 3 factors you would get
 products, but there are many repeats. products, but there are many repeats.
There is just one way to get  , ,  , , 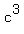 , , 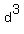 and and  , ,
but there are several ways to make 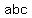 , ,
and there are several ways to make many other products like 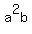 and and 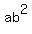 . .
Rather than writing all repeats of the same product, we can list them grouped, sort of like 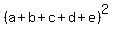 above. above.
There are  possible 3-different-letter combination products, and each one will appear repeated possible 3-different-letter combination products, and each one will appear repeated  times, times,
accounting for  of the of the  products. products.
How do we know there are  possible 3-different-letter combinations? possible 3-different-letter combinations?
Your teacher may say that it is combinations of 5 taken 3 at a time,
and that you can calculate that as  , ,
but it is easy enough to list them and count them.
Where does the  times come from? times come from?
How many ways can we make 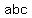 ? ?
You could choose the  from the first from the first 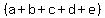 factor, or from the second one, or from the third one. factor, or from the second one, or from the third one.
After that you would still have two choices for the  , ,
and there would be  ways to make ways to make 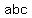 . .
Your teacher may say that it is permutations of 3, or 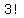 . .
The same goes for 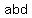 , , 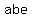 , ,  , etc. , etc.
As for products like 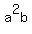 , there are , there are  possible sets of 2 letters, but the same 2 letters can make 2 such products, so there are possible sets of 2 letters, but the same 2 letters can make 2 such products, so there are  such products. such products.
Each of those products can be made  different ways, different ways,
because there are 3 factors where you can find the letter that is not squared.
That accounts for  of the of the  products. products.
All in all, counting all repeats, we have
 cubes, cubes,
 factors with one letter squared, and factors with one letter squared, and
 factors with no exponents, factors with no exponents,
adding up to the  expected factors. expected factors.

|
|
|