SOLUTION: How to prove if this question is to be asked for a triangle: prove that x=y=pi/3 given that {{{cos x+cos y-cos(x+y)=3/2 }}}

Algebra ->  Trigonometry-basics -> SOLUTION: How to prove if this question is to be asked for a triangle: prove that x=y=pi/3 given that {{{cos x+cos y-cos(x+y)=3/2 }}}       Log On


   

Question 883143: How to prove if this question is to be asked for a triangle: prove that x=y=pi/3 given that cos+x%2Bcos+y-cos%28x%2By%29=3%2F2++
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
cos%28x%29%2Bcos%28y%29-cos%28x%2By%29=3%2F2

cos%28x%29%2Bcos%28y%29-%28cos%28x%29cos%28y%29-sin%28x%29sin%28y%29%29=3%2F2

cos%28x%29%2Bcos%28y%29-cos%28x%29cos%28y%29%2Bsin%28x%29sin%28y%29=3%2F2



Let a = cos(x), b = cos(y) 

a%2Bb-ab+%2B-+sqrt%281-a%5E2%29sqrt%281-b%5E2%29=3%2F2



%28a%2Bb-ab+-3%2F2%29%5E2+=+%281-a%5E2%29%281-b%5E2%29



2a%5E2b-2a%5E2%2B2ab%5E2-5ab%2B3a-2b%5E2%2B3b-5%2F4+=+0

8a%5E2b-8a%5E2%2B8ab%5E2-20ab%2B12a-8b%5E2%2B12b-5+=+0

8a%5E2b-8a%5E2%2B8ab%5E2-20ab%2B12a-8b%5E2%2B12b-5+=+0

%288b-8%29a%5E2%2B%288b%5E2-20b%2B12%29a%2B%28-8b%5E2%2B12b-5%29+=+0

8%28b-1%29a%5E2%2B4%282b%5E2-5b%2B3%29a%2B%28-8b%5E2%2B12b-5%29+=+0

8%28b-1%29a%5E2%2B4%282b-3%29%28b-1%29a%2B%28-8b%5E2%2B12b-5%29+=+0

That's a quadratic in a, and the solutions must be
real, so the discriminant must be non-negative, so

4%5E2%282b-3%29%5E2%28b-1%29%5E2-4%2A8%28b-1%29%28-8b%5E2%2B12b-5%29%3E=0

16%282b-3%29%5E2%28b-1%29%5E2-32%28b-1%29%28-8b%5E2%2B12b-5%29%3E=0

%282b-3%29%5E2%28b-1%29%5E2-2%28b-1%29%28-8b%5E2%2B12b-5%29%3E=0

%28b-1%29%28%282b-3%29%5E2%28b-1%29-2%28-8b%5E2%2B12b-5%29%29%3E=0

%28b-1%29%28%284b%5E2-12b%2B9%29%28b-1%29%2B16b%5E2-24b%2B10%29%3E=0

%28b-1%29%284b%5E3-12b%5E2%2B9b-4b%5E2%2B12b-9%2B16b%5E2-24b%2B10%29%3E=0

%28b-1%29%284b%5E3-3b%2B1%29%3E=0

We factor the cubic in the parentheses. 
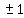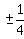It has possible rational zeros %22%22+%2B-+1, %22%22+%2B-+1%2F2, %22%22+%2B-+1%2F4.

It's easy to see that -1 is a zero.  So

-1|4  0 -3  1
  |  -4  4 -1
   4 -4  1  0

So we have further factored the expression 
on the left as

%28b-1%29%28b%2B1%29%284b%5E2-4b%2B1%29%3E=0 

and we factor once more as

%28b-1%29%28b%2B1%29%282b-1%29%5E2%3E=0

The critical numbers are the zeros of the
left side, which are 1, -1, and 1/2

Put those on a number line, test the intervals,
and the critical values, and get the graph of 
solution inequality as:

<============●-----●-●===========>
-4  -3  -2  -1   0 1%2F21   2   3   4

(-infinity,-1] U %22%7B%221%2F2 }  U [1,infinity)

Since b = cos(x), and -1%3C=cos%28x%29%3C=1, we have 

cos(x)=-1, cos(x)=1%2F2, cos(x)=1
     x=pi,       x=pi%2F3,     x=0

The only possibility for x is pi%2F3.

Interchange x and y in the above and 
we get y = pi%2F3      

Interchange x and z in the above and 
we get z = pi%2F3.

So all three angles are pi%2F3 and so
the triangle is equilateral. 

Edwin