Question 882930: a Polynomial P(x) and a divisor d(x) are given. Use long division to find the quotient Q(x) and the remainder R(x) when P(x) is divided by d(x), and express P(x) in the form d(x)*Q(x)+R(x)


Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SOLUTION:
 , ,  , and P(x) in the form d(x)*Q(x)+R(x), or , and P(x) in the form d(x)*Q(x)+R(x), or
 , is , is  . .
THE LONG DIVISION:
The format for long division varies from country to country (and maybe even from teacher to teacher. I will use the format my children were taught in the USA.
The first term of quotient 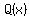 is the quotient of the first terms is the quotient of the first terms  . .
Then  is subtracted from is subtracted from  . .
Subtracting 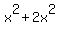 is adding is adding  , ,
and the result is
 . .
That is shown below, but I am saving room for terms in  by including the term by including the term   . .
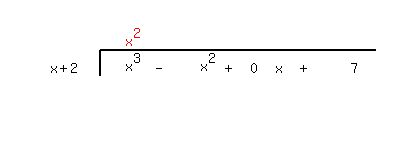 ---> --->
We continue dividing by  the remaining the remaining 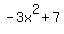 , ,
which I wrote as 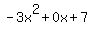 to save room for the term in to save room for the term in  . .
The next term in the quotient, which comes from dividing first terms, is
 . .
That term, times the divisor is
 , which must be subtracted from , which must be subtracted from
 . .
Subtracting 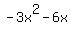 is adding is adding  , ,
and the result is  . .
 ---> --->
To find the next term of 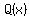 , ,
we have to divide the first term of the remaining 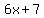
by the first term of divisor  : :
 . .
So the last term of the quotient will be  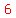 , ,
and we need to subtract the product
 from the remaining from the remaining 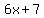 . .
Since subtracting 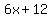 is adding is adding  , ,
I add 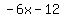 to that remaining to that remaining 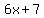 and find the remainder: and find the remainder:
 : :
 ---> --->
|
|
|