SOLUTION: If 180° < A < 270° and cos(A) = 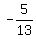{{{-5/13}}}, solve for the value of tan(A)

Since , A is in quadrant 3 we draw a right triangle in quadrant 3.  
Label the side on the x-axis as x, the vertical side y, and the hypotenuse as r.
Indicate the angle A with a red curved line rotating counter-clockwise from the
right side of the x-axis, to the terminal side, which is the hypotenuse r.



Since  we take x to be the numerator of  which is -5, 
and r to be the denominator of   which is 13.



Then we calculate y by the Pythagorean theorem:







Since y goes down from the x-axis, we take the
negative value for y as -12




Now since the 



Edwin