|
Question 881931: In a round trip, a plane flies 990 miles each way,one way with tailwind and one with headwind. The total trip time is 3 hours and 20 mins. The airspeed of the plane is 600 miles/hour. What is the speed of the wind?
To me, this seems extremely bizarre and I am wondering where the heck did the speed of wind come into the question
In no rush for the answer and thanks in advanced for your help!
Found 3 solutions by richwmiller, jim_thompson5910, MathTherapy:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a common type travel problem
a+b=3 1/3
r*t=d
The speed one way will be 600 + plus the wind and the other way 660 minus the wind.
They assume the speed of the wind is constant.
We have three unknowns: the speed of the wind and the time in each direction.
(600+w)*a=990,
(600-w)*b=990,
a+b=3 1/3
a=3 1/3-b
(600+w)*(3 1/3-b)a=990,
(600-w)*b=990
a = 3/2, b = 11/6, w = 60
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a round trip, a plane flies 990 miles each way,one way with tailwind and one with headwind. The total trip time is 3 hours and 20 mins. The airspeed of the plane is 600 miles/hour. What is the speed of the wind?
To me, this seems extremely bizarre and I am wondering where the heck did the speed of wind come into the question
In no rush for the answer and thanks in advanced for your help!
Let speed of wind be S
With a tailwind, the plane's total speed is: 600 + S
With a headwind, the plane's total speed is: 600 - S
Since outbound TIME, plus return TIME, equals 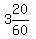 , or , or  , or , or  hours, then we can say that: hours, then we can say that:


990(3)(600 - S) + 990(3)(600 + S) = 10(600 + S)(600 – S) ------- Multiplying by LCD, 3(600 + S)(600 – S)






(S - 60)(S + 60) = 0
S, or speed of wind =  mph OR S = - 60 (ignore) mph OR S = - 60 (ignore)
|
|
|
| |