|
Question 881310: A cow is tied to a corner of a fenced rectangular plot of length 40m and breadth 14m.The length of the rope is 21m.Find the total area that it can graze?
I want proper solution with figure.
Found 3 solutions by Fombitz, Theo, KMST:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your proper diagram is shown here:
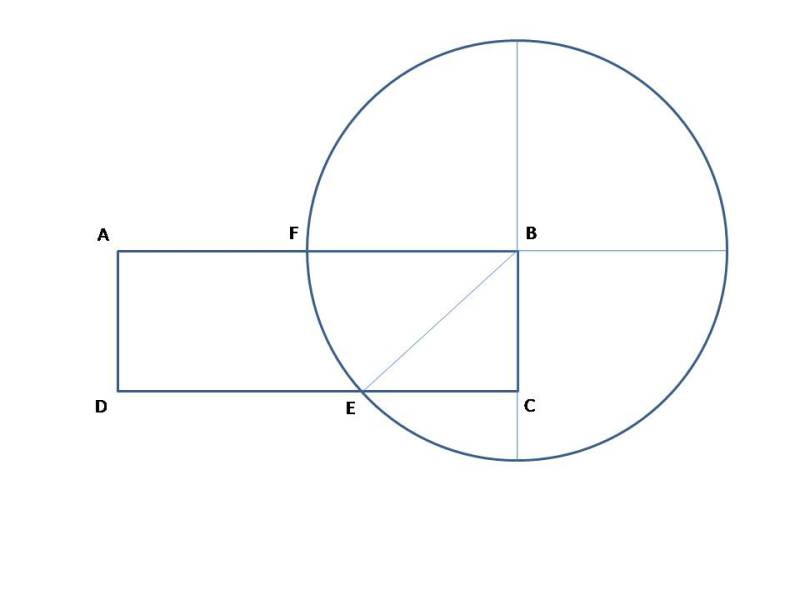
the measurements that are important are:
1. area of the circle.
2. area of triangle EBC
3. area of sector of the circle FBE
the area that the cow can graze on would be:
area of the circle minus the area of triangle EBC minus the area of sector FBE.
the area of the circle is equal to pi * r^2 which is equal to pi * 21^2 which is equal to 1385.44236
all intermediate values are stored in memory of my calculator so that there is no rounding until the final results are posted which you can round to whatever number of decimal places you need.
the area of triangle EBC depends on the length of line segment EC which is not provided but can be calculated in a couple of ways.
i'll use trigonometry to figure it out since i need the angle EBC in order to find angle FBE anyway.
the line segment EB is equal to 21 which is the radius of the circle.
the line segment BC is the breadth of the rectangle which is equal to 14.
the cosine of angle EBC is equal to 14/21.
angle EBC is therefore equal to the arc cosine of (14/21) which is equal to 48.1896851 degrees.
since angle FBC is a right angle, this makes angle FBE equal to 90 - 48.1896851 which makes angle FBE equal to 41.8103149 degrees.
that information is held for later when calculating the area of sector of the circle FBE.
since angle EBC is equal to 48.1896851 degrees, we can now find the length of line segment EC because the sine of angle EBC is equal to opposite divided by hypotenuse which is equal to EC / EB.
the formula is:
sine of angle EBC equals EC divided by EB which becomes:
sine of 48.1896851 = EC / 21.
solving for EC, we get:
EC = 21 * sine of 48.1896851 which is equal to 15.65247584
we now have enough information to find the area of triangle EBC
the area of triangle EBC is equal to 1/2 * the base * the height.
this makes the area of triangle EBC equal to 1/2 * EC * BC which is equal to
1/2 * 14 * 15.65247584 which becomes which is equal to 109.5673309.
the area of triangle EBC is equal to 109.5673309.
now we need to find the area of the sector of the circle marked FBE.
the formula for area of a sector is equal to angle of the sector divided by 360 * area of the circle.
the angle of the sector is what we calculated previously which is the angle of FBE which is equal to 41.8103149 degrees.
the area of the sector FBE is therefore equal to:
41.8103149 / 360 * 1385.44236 which is equal to 160.9049482
we have all the information we need now.
the area of the circle is equal to 1385.44236
the area of triangle EBC is equal to 109.5673309
the area of sector FBE is equal to 160.9049482
from this information, the area that the cow can graze on is:
area of circle minus area of triangle EBC minus area of sector FBE which is equal to:
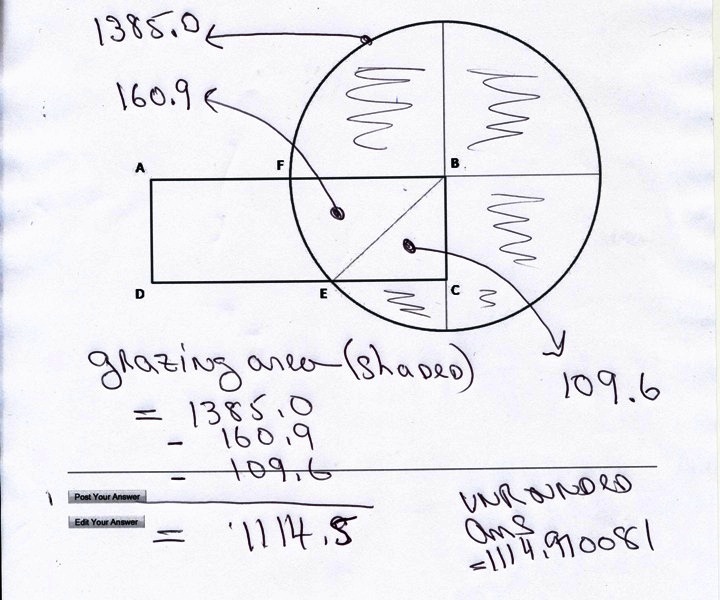
1385.44236 minus 109.5673309 minus 160.9049482 which is equal to 1114.970081.
the following picture shows the results of all calculations rounded to 1 decimal place so as not to clutter up the picture too much with details that you already have from the calculations above.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the popular problem where the cow is tied to the corner of a rectangular restricted area, the cow is on the outside and is tied to the corner of a barn.
Your cow may be tied inside a fenced rectangular plot, and that would be a different problem.
I'll discuss both, but see if I make sense, and see if I calculated right, because I am prone to making mistakes.
If the cow is inside that rectangular plot:
 With the rope tight, a cow, tied at With the rope tight, a cow, tied at  , can circle from , can circle from  to to 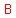 . .
So the cow can graze the X-centered wedge from A to B. and the right triangle XYB.
We can find the angle YXB from  . .
That angle measures about 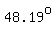 . .
The sine of that angle is  , ,
so the area of triangle XYB (in square meters) is
 = approx. = approx. 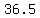 square meters. square meters.
The area of a 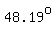 wedge is wedge is  of the area of the full circle., so the area of the XAB wedge, in square meters is about of the area of the full circle., so the area of the XAB wedge, in square meters is about
 . .
Then, the total area the cow can graze, in square meters, is about
 . .
If the cow is outside that rectangular plot, and allowed to graze as far as the rope will allow;
 With the rope tight, a cow, tied at With the rope tight, a cow, tied at 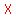 , can circle from , can circle from 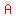 to to 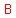 , and then to , and then to  . .
The cow can graze on  of the 21-m radius circle centered at of the 21-m radius circle centered at 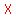 , ,
and also on  of a 7-m radius circle centered at of a 7-m radius circle centered at 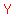 . .
The total area, in square meters, is:
 . .
That is about 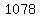 square meters. square meters.
|
|
|
| |