suppose that you drop a ball from a window 45m above the ground. The ball bounces to 65% of it previous height wit each bounce. Find the total number of metres the ball travels between the time it is dropped and the 8th bounce.
It is not clear what is meant exactly by
"between the time it is dropped and the 8th bounce.".
Does this mean that we are to determine the number of meters the ball
has traveled when it hits the ground the 8th time? or the 9th time?
We really cannot be sure! You will have to ask your teacher.
I will arbitrarily assume it is like the drawing below, and find the distance
the ball has traveled when it hits the ground for the 8th time, not the 9th.
As you see from the sketch, there are 8 "falls" and 7 "rises".
The "falls" form a geometric series, with a1=45, r=0.65, n=8
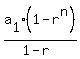
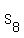
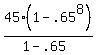
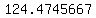So the sum of the 8 "falls" is 124.47456669m.
The sum of the "rises" is the same as the sum of the "falls" except for the
first "fall" of 45m.
So the sum of the rises is 124.47456669m - 45m = 79.47456669m
Distance the ball has traveled when it hits the ground the 8th time =
124.47456669m + 79.47456669m = 203.9491334m.
Edwin
