SOLUTION: A can do a piece of work in 2/3 as many days as B, and B can do the same work in 4/5 as many days as C. Together they can do the work in 3 7/11 days. In how many days can A do the

Algebra ->  Rate-of-work-word-problems -> SOLUTION: A can do a piece of work in 2/3 as many days as B, and B can do the same work in 4/5 as many days as C. Together they can do the work in 3 7/11 days. In how many days can A do the       Log On


   

Question 880396: A can do a piece of work in 2/3 as many days as B, and B can do the same work in 4/5 as many days as C. Together they can do the work in 3 7/11 days. In how many days can A do the work alone?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

A can do a piece of work in 2/3 as many days as B, and B can do the same work in 4/5 as many days as C. Together they can do the work in 3 7/11 days. In how many days can A do the work alone?
Suppose C can do one complete job in x days.

Then C's work rate in jobs per day is

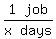
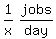
matrix%281%2C2%2C1%2Cjob%29%2Fmatrix%281%2C2%2Cx%2Cdays%29%22%22=%22%22matrix%281%2C2%2C1%2Fx%2Cjobs%2Fday%29

B can do the same work in 4/5 as many days as C

So B can do the job in 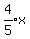expr%284%2F5%29x days.

Then B's work rate in jobs per day is

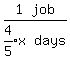
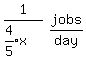matrix%281%2C2%2C1%2Cjob%29%2Fmatrix%281%2C2%2Cexpr%284%2F5%29x%2Cdays%29%22%22=%22%22matrix%281%2C2%2C1%2F%28expr%284%2F5%29x%29%2Cjobs%2Fday%29

Simplify that compound fraction by multiplying top and bottom by 5

So B's work rate is

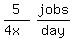
matrix%281%2C2%2C5%2F%284x%29%2Cjobs%2Fday%29

A can do a piece of work in 2/3 as many days as B

Since B can do the job in 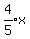expr%284%2F5%29x days,

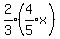A can do the job in expr%282%2F3%29%28expr%284%2F5%29x%29 days.

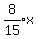So A can do the job in expr%288%2F15%29x days

---

Then A's work rate in jobs per day is

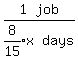
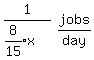matrix%281%2C2%2C1%2Cjob%29%2Fmatrix%281%2C2%2Cexpr%288%2F15%29x%2Cdays%29%22%22=%22%22matrix%281%2C2%2C1%2F%28expr%288%2F15%29x%29%2Cjobs%2Fday%29

Simplify that compound fraction by multiplying top and bottom by 15

So A's work rate is

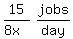matrix%281%2C2%2C15%2F%288x%29%2Cjobs%2Fday%29

---

Together they can do the work in 3 7/11 days.
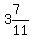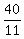Change 3%267%2F11 to improper fraction 40%2F11

Then all three's combine work rate in jobs per day is

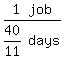
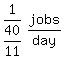matrix%281%2C2%2C1%2Cjob%29%2Fmatrix%281%2C2%2Cexpr%2840%2F11%29%2Cdays%29%22%22=%22%22matrix%281%2C2%2C1%2Fexpr%2840%2F11%29%2Cjobs%2Fday%29

Simplify that compound fraction by multiplying top and bottom by 11

So their combined work rate is

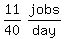matrix%281%2C2%2C11%2F40%2Cjobs%2Fday%29

---

The equation comes from:

%22%22%2B%22%22%22%22%2B%22%22 %22%22=%22%22 



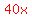Multiply through by the LCD of red%2840x%29:





matrix%281%2C5%2C%0D%0A165%2C%22%22%2C%22%22=%22%22%2C%22%22%2C11x%29

matrix%281%2C5%2C%0D%0A165%2F11%2C%22%22%2C%22%22=%22%22%2C%22%22%2Cx%29

matrix%281%2C5%2C%0D%0A15%2C%22%22%2C%22%22=%22%22%2C%22%22%2Cx%29

So C can finish the job in 15 days.

The qustion is:

In how many days can A do the work alone?
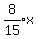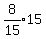A can do the job in expr%288%2F15%29x days, or expr%288%2F15%2915

or 8 days.  That's the answer.

------------------------------------

To check we need how many days it takes B to do the job alone:

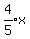B can do the job in expr%284%2F5%29x days.

That's expr%284%2F5%2915%29 or 12 days.

To check, add their rates in jobs per day to see if we get 11%2F40



That checks, so we are right.

A can complete the job in 8 days.

Edwin