Question 880388: Me again.
Hi - I know this is probably really simple, are I do not know if I am on the right track for this question (probability is just not making any sense to me at all).
It is known that 25% of all staff in a company make use of the free influenza vaccination programme. Answer the following as: The probability is equal to: (Round your probability to 4 decimal places:
Q If 20 people are randomly selected, find the probability that exactly 12 people don't use the vaccination programme.
Please help!
Thanks in advance!
Found 2 solutions by ewatrrr, KMST:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think we are all reading it wrong.
THE ANSWER:
Maybe you just want the answer. In that case, I calculated the approximate probability that 12 of those 20 people got vaccinated as
 , but I think you may really have meant what is the probability that , but I think you may really have meant what is the probability that  of the of the  were not vaccinated. were not vaccinated.
Then, it would be

THE CALCULATION:
Maybe you want to know how to calculate it.
If you have a computer with the right software, or a calculator with enough functions, you can calculate combinations of 20 taking 12 at a time as 20C12= . .
With a simpler calculator, or (gasp!) with pencil and paper,
you would calculate it as
20C12=20C8= . .
With most calculators or using your computer you can calculate  (approximately) and (approximately) and
 (approximately). (approximately).
Then you calculate your approximate probability as
 , which rounds to , which rounds to  . .
With pencil and paper it gets a little more cumbersome.
THE REASON WHY YOU APPLY "THE BINOMIAL DISTRIBUTION":
Maybe you want to understand why.
You can describe all the possible outcomes of randomly picking  of the people in the staff of that company by the binomial of the people in the staff of that company by the binomial
 , meaning that , meaning that
there is a 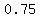 probability that he/she got the vaccine and probability that he/she got the vaccine and
there is a 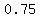 probability that he/she did not get the vaccine. probability that he/she did not get the vaccine.
If you pick  people, you can describe all the possible outcomes as the square of that binomial: people, you can describe all the possible outcomes as the square of that binomial:
 . .
That means there is a 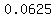 probability that both goth the vaccine; probability that both goth the vaccine;
there is a  probability that one or the other (got the vaccine(but not both), probability that one or the other (got the vaccine(but not both),
and there is a  probability that both are unvaccinated. probability that both are unvaccinated.
If you pick  people, the whole spectrum of probabilities is described by the 20th power of that binomial: people, the whole spectrum of probabilities is described by the 20th power of that binomial:

In that long polynomial, the coefficient of the term with  represents the probability that exactly represents the probability that exactly  of those of those  people were vaccinated, and the other people were vaccinated, and the other  did not use he vaccination programme. did not use he vaccination programme.
|
|
|