Question 880271: If sin^4(theta)=cos^5(theta),then what is the value of 'theta' ?
Answer by DrBeeee(684)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm not sure there is an analytical solution. I spent a few minutes trying to derive one but gave up and solved it by iteration. That is, select an initial value of theta and iterively converge to a more precise value.
Using x instead of theta, the given expression is
(1)  or by dividing each side by or by dividing each side by 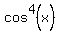 we get we get
(2)
Since the absolute value of the cosine function is less than or equal to one, and the tan(45) is one, start x at 45 degrees and get
(3) at x = 45, LS = 1, RS = .335, note that LS is greater than the RS
Now decrease x,
(4) at x = 40, LS = .4957, RS = .766, note LS is now less than RS, we went too far, so x lies between 40 and 45.
(5) at x = 43, LS = .756, RS = .731, LS is greater than RS, now x is between 40 and 43.
(6) at x = 42.5 LS = .7050, RS = .7372 LS is less than RS, went too far, now x is between 42.5 and 43.
Keep doing this until you get to
(7) x = 42.78634
To check this use (1)
Is ( )? )?
Is (0.212892 = 0.212892)? Yes
Answer; theta equals approximately 42.78634 degrees.
|
|
|