|
Question 87946: if I have the height and volume of a cylinder, how do I find the radius? or diameter?
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume of a cylinder is found by multiplying the area of the circular base times the
height. And the area of the circular base can be written two ways depending on whether
you choose the diameter or the radius to work with. Let A = area, R = radius, and D = diameter.
Then the area of a circle is either:
.

.
or by recognizing that the radius is half the diameter  and then substituting and then substituting
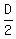 for R in the above Area equation you get: for R in the above Area equation you get:
.

.
Next the Volume (V) of the cylinder is just the height (H) times A or H*A. Substituting
for A we can write:
.

.
or
.

.
Now all you have to do is to plug in the values that you are given for V and H and solve
for either R or D. Let's work a couple of examples. (Make sure you use a consistent
set of units. If the height is in inches, then you need the volume in cubic inches
and the diameter and radius will be in inches also. The area will be square inches.)
.
Suppose you are given that the volume is 400 cubic inches (V = 400) and the height is
10 inches. To find the radius, use the equation:
.

.
Substitute 400 for V and 10 for H and you get:
.

.
Now divide both sides by the multipliers of 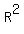 and you get: and you get:
.

.
and solve for R by taking the square root of both sides:
.

.
If you use your calculator to find 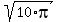 you find that you find that 
and the square root of that is  . Substituting this into the equation . Substituting this into the equation
gives you:
.

.
and since we are working in inches, our answer is in inches also.
.
You can find the diameter by just multiplying the answer for R by 2 to get 7.136496465
inches or you can use the equation that we got above involving the volume and the diameter.
Let's use the equation:
.

.
Substitute 400 for V and 10 for H to get:
.

.
Multiply both sides of this equation by 4 to get rid of the denominator on the right side.
When you do that, the equation becomes:
.

.
Divide both sides by  and the equation simplifies to: and the equation simplifies to:
.

.
Use a calculator to determine that  . This reduces the . This reduces the
equation to:
.

.
Finally, by taking the square root of both sides, you get:
.

.
and 7.136496465 inches for the diameter is the same answer that we got above by doubling
the radius, so it checks.
.
Hope this helps you. If you study the problem, as complex as it seems, all you have to
know is the formulas for the area of a circle and the fact that the volume of a cylinder is
found by multiplying the circular area of the cylinder times the height of the cylinder.
The rest of the problem just consists of plugging in the values you are given and solving
the resulting equation.
|
|
|
| |