Question 879033: Organizers for a high school graduation have set up chairs in two sections. They put 126 chairs for the graduates in the front section and 588 chairs for guests in the back section. If all rows have the same number of chairs, what is the greatest number of chairs possible for a row?
Answer by JulietG(1812)   (Show Source): (Show Source):
You can put this solution on YOUR website! What is the great common factor of 126 and 588?
Factors of 126 = 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.
Factors of 588 = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 49, 84, 98, 147, 196, 294, 588.
The great number they have in common is 42. Assuming all rows to be equal (42 chairs per row), there will be:
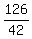 rows of chairs for the graduates [3 rows], and rows of chairs for the graduates [3 rows], and
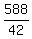 rows of chairs for the guests [14 rows] rows of chairs for the guests [14 rows]
|
|
|