Question 879030: I am trying to find the sum of the following sequence:32+33+34+35+...+113. I can do any when it starts with 1, but I cannot grasp how to solve this one.
Thank you
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625)   (Show Source):
You can put this solution on YOUR website! You can derive a specific expression for the sum, without using the formula, if you want.
How many terms are in your sum? You see the difference between terms is 1; if you only had 32+33+34, this is three terms to sum. 34-32=2, but add 1 more to get 3; meaning three terms. YOUR given summation uses (113-32)+1=82 terms.
Now if you had, 32+33+34, and you add to it 34+33+32, you can show:
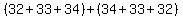
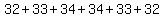
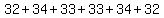
 , commutative property for addition
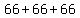
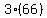
In partial wording, 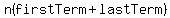 , and n is for how many terms in the sum. YOUR sum has first term 32 and last term 113, and since the little example I showed was for DOUBLE the sum, you want to divide by 2:
-
-
Your example has n=82, firstTerm=32, lastTerm=113.
The sum wanted is 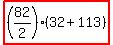 . Just compute the number.
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
I am trying to find the sum of the following sequence:32+33+34+35+...+113. I can do any when it starts with 1, but I cannot grasp how to solve this one.
Thank you
Sum of A.P. ( ) when n, or number of terms, 1st term , or ( ), and last term ( ) are known: 
Number of terms: 113 - 32 + 1, or 82
Therefore, becomes:  , or  , or 
You can do the check!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
|
|
|
