Question 878798: This question is a homework question but I think that the formula is wrong. I could be wrong though. I need someone to PLEASE work me through this because I honestly have no clue what to do.
Travis is riding the Ferris wheel at the amusement park. His height can be modeled by the equation
H(t) = 22 cos (pi over 13)t + 28, where H represents the height of the person above the ground in feet at t seconds.
Part 1: How far above the ground is Travis before the ride begins?
Part 2: How long does the Ferris wheel take to make one complete revolution?
Part 3: Assuming Travis begins the ride at the top, how far from the ground is the edge of the Ferris wheel, when Travis' height above the ground reaches a minimum?
part 1 I believe is 28. Part 2 doesn't make sense to me. since t is outside of the parenthesis, wouldn't it take forever to make a full rotation? I don't think the formula is correct. For part three, would it be 13? I am saying that because of the 13 that appears in the equation. Although I think I am wrong. I am never any good with trigonometry or formulas. I need some help with this pretty please! I would really appreciate it!!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe that you may have asked the same question twice and already received a technically appropriate answer.
However, in case you are one of two people who asked the exact same question, or if you want to see an answer with a different flavor, I will give you my kind of answer.
The function is not clear from your writing, but I expect that it is not  , ,
because  , with , with  makes more sense: makes more sense:

 , where , where 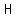 represents the height of the person above the ground in feet at represents the height of the person above the ground in feet at  seconds means that seconds means that
at  (when the time count starts), (when the time count starts),

Part 1: How far above the ground is Travis before the ride begins?
If "before the ride begins" means at  , then Travis is , then Travis is  above the ground "before the ride begins." above the ground "before the ride begins."
Part 2: How long does the Ferris wheel take to make one complete revolution?
One complete revolution after  , ,  again. That means again. That means
 --> --> --> --> --> --> --> --> --> -->
As  increases from increases from  , ,
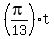 increases from increases from  , ,
and  changes from changes from  . .
The first time  again is when again is when  , and , and
 --> --> --> --> --> -->
So it takes  for the Ferris wheel to make one complete revolution. for the Ferris wheel to make one complete revolution.
Part 3: Assuming Travis begins the ride at the top, how far from the ground is the edge of the Ferris wheel, when Travis' height above the ground reaches a minimum?
That is one unrealistic question.
What does "the height of the person above the ground" mean?
It could not be the height of the person's head, because it would depend on how tall the person is.
It could be the height of the seat bottom that person is on, but that could be above, below or to the side of "the edge of the Ferris wheel" depending on the Ferris wheel design.
To make sense of the problem, we have to assume that "the height of the person above the ground" means the height of the axle of the passenger carrying gondola, and that the axle is attached to "the edge of the Ferris wheel."
So  would be the the height above the ground in feet of the edge of the wheel (at the point where the gondola is attached) at would be the the height above the ground in feet of the edge of the wheel (at the point where the gondola is attached) at  seconds. seconds.
The minimum of  occurs when occurs when  is minimum. is minimum.
Since  the minimum of the minimum of  happens when happens when  , ,
and at that time  . .
So when Travis' height above the ground reaches a minimum, the edge of the Ferris wheel is  above the ground. above the ground.
|
|
|