Question 878782: A cube has all of its sides painted in blue and then is cut into 1000 cubes of the same size. All cubes are placed in an urn and are thoroughly mixed, so that the probability of being randomly picked from the urn is the same for all cubes. What is the probability that a randomly picked cube has at least one of its sides painted blue?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! After you cut the cube into 1000 smaller cubes of the same size, you notice that each original edge has been split into 10 small cube edges, and each blue face has been split into 100 small cube faces.
We could peel away all the partially painted little cubes on the outside of the original cube, put them aside on a pile and count them.
We would find that there are 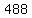 such partially painted little cubes. such partially painted little cubes.
The "core" unpainted cube left over has edges made up of o small cube edges, and contains the remaining
 small cubes. small cubes.
When all small cubes are placed in the urn and mixed,
 or or  of the small cubes in the urn are partially painted, of the small cubes in the urn are partially painted,
so the probability that a randomly picked small cube has at least one of its sides painted blue is
 or or  . .
How can we count the partially painted little cubes?
I just calculated the number of small cubes in the "core" edge left after peeling off the painted outside cubes, and subtracted the result from 1000.
Since I had peeled away
the  outside layers of partially painted small cubes on the left and right sides, outside layers of partially painted small cubes on the left and right sides,
the  outside layers of partially painted small cubes on the front and back, and outside layers of partially painted small cubes on the front and back, and
the  outside layers of partially painted small cubes on the top and bottom, outside layers of partially painted small cubes on the top and bottom,
what was left was an unpainted cube with  small cubes per edge. small cubes per edge.
 cubes per layer in cubes per layer in  layers, layers,
and  cubes in all. cubes in all.
Then  . .
I could also have counted the partially painted little cubes as I peeled them off the original, larger cube.
There were  on the corners (with 3 painted faces). on the corners (with 3 painted faces).
After taking the corner small cubes off, I took off the remaining small cubes on the 12 edges. There were 8 left on each edge, and each one had 2 painted faces.
There were  of those, of those,
Finally, I took of the small partially painted cubes left in the middle of each of the 6 faces of the cube. They had only one face painted, and they were covering the 8 small cube by 8 small cube square in the middle of each face.
There were  on each face, and on each face, and  in all. in all.
The total number of peeled off partially painted small cubes was
 . .
I could also have counted the partially painted little cube faces, and then corrected for the double and triple contributions to that total from the little cubes with more than one painted face.
Each of the 6 large cube faces is s;pit into  small cube painted faces, for a total of 6*100=600 painted faces. small cube painted faces, for a total of 6*100=600 painted faces.
There were  small cubes on the corners, with 3 painted faces, on the corners of original large cube. Those small cubes on the corners, with 3 painted faces, on the corners of original large cube. Those  corner little cubes account for corner little cubes account for  of the painted faces, so when counting faces, I am counting too many. To correct my count I have to subtract of the painted faces, so when counting faces, I am counting too many. To correct my count I have to subtract  . .
There are also  small cubes on the middle of each of the 12 edges that have 2 painted faces. Those are small cubes on the middle of each of the 12 edges that have 2 painted faces. Those are  cubes that had 2 faces counted in the total count of painted faces. To correct my count I have to subtract cubes that had 2 faces counted in the total count of painted faces. To correct my count I have to subtract 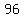 from the total- count of painted faces. from the total- count of painted faces.
Calculated that way, the total number of partially painted small cubes is
 . .
I like it when I can get the same result two or three different ways. It makes me more confident that I did not make a mistake.
|
|
|