Question 878714: The area of a right triangle is 84 cm2. If four times length of one leg is 3 cm longer than the length of the hypotenuse, what are the measures of the three sides?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! GUESS AND CHECK STRATEGY:
If you are not that deep into algebra and calculus, you are expected to try whole numbers for the lengths of the sides in centimeters.
The area given is a clue. It is related to the product you get by multiplying the legs' lengths in centimeters.
For a right triangle, you can take the length of one leg as the base, and the length of the other leg as the height, so
  
 -->  --> 
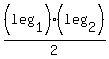
We look for pairs of factors of 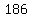 that could be the legs' lengths in centimeters.
We know that 
 sounds like a good possibility, because a hypotenuse so much longer that the "one leg" means that the other leg must also be much longer than the "one leg".
In a right triangle with legs measuring  and  , the hypotenuse measures
Is "four times" "3 more than"  ?
YES. 
So the lengths of the sides are  ,  , and  .
Another way (no calculations involved, but your teacher may consider it cheating) would be to look up a list of Pythagorean triples. Those are sets of whole numbers that could be the lengths of the sides of a right triangle. (The squares of the first two numbers add up to the square of the third number).
One of those triples is 7 24 25, and it is the only one where 7 appears as a factor, and the two first numbers are factors of 186.
NOT GUESS AND CHECK?
Then you may have to start writing equations and may loose sight of the triangle issue.
|
|
|
