SOLUTION: find the length of x its a triangle right side is 51 ft left side is x and bottom is 45 ft

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: find the length of x its a triangle right side is 51 ft left side is x and bottom is 45 ft      Log On


   

Question 87841: find the length of x
its a triangle
right side is 51 ft left side is x and bottom is 45 ft
Found 2 solutions by jim_thompson5910, Earlsdon:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Since we have a triangle with legs of 51 , 45 and a hypotenuse of x(our unknown side), we can use Pythagoreans theorem to find the unknown side.
Pythagoreans theorem
a%5E2%2Bb%5E2=c%5E2

51%5E2%2B45%5E2=x%5E2 Plug in a=51, b=45, and c=x and lets solve for x
2+6+0+1+%2B+2+0+2+5+=++x++%5E+2 Square each individual term



4+6+2+6+=++x++%5E+2 Combine like terms


s+q+r+t+%28+4+6+2+6+%29+=+s+q+r+t+%28++x++%5E+2+%29 Take the square root of both sides


s+q+r+t+%28+4+6+2+6+%29+=+x Simplify

So our answer is
x+=+s+q+r+t+%28+4+6+2+6+%29

which approximates to

x=68.014704292527

Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
With the limited information you have supplied, x could be any number with the following constraints:
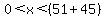
0%3Cx%3C%2851%2B45%29
Do you see why this is so?
Imagine two sticks, one 51 ft. long and the other 45 ft. long. Imagine that these sticks are joined at one end by a hinge that allows you to open and close them like a door.
Well, let's say that you can join the two unconnected ends together with another stick whose length is x ft to form a triangle.
You can easily see that the length of x depends entirely upon how wide open the two sticks are, doesn't it?
So, to find the length of x, you need to provide an angle.
Is the triangle a right-triangle?
If it is, then you can use the Pythagorean Theorem to figure out the length of x.
Let's assume that you forgot to mention that it is a right triangle. We can find the length of x using the Pythagorean Theorem: c%5E2+=+a%5E2%2Bb%5E2
But to do this, we have to make another assumption about which side is the hypotenuse...is it 51 ft. or is it x ft. (It can't be 45 ft because the hypotenuse of a right triangle is always the longest side).
Let's assume that x is the hypotenuse, then:
x%5E2+=+51%5E2%2B45%5E2
x%5E2+=+4626 x+=+68 feet.
Now let's assume that 51 ft is the length of the hypotenuse, then:
51%5E2+=+x%5E2+%2B+45%5E2
2601+=+x%5E2%2B2025
x%5E2+=+2601-2025
x%5E2+=+576
x+=+24 feet.