SOLUTION: An artist needs to know the area of a triangular piece of stained glass with sides measuring 9 cm, 7 cm, and 5 cm. What is the area to the nearest square centimeter?

Algebra ->  Trigonometry-basics -> SOLUTION: An artist needs to know the area of a triangular piece of stained glass with sides measuring 9 cm, 7 cm, and 5 cm. What is the area to the nearest square centimeter?      Log On


   

Question 877138: An artist needs to know the area of a triangular piece of stained glass with sides measuring 9 cm, 7 cm, and 5 cm. What is the area to the nearest square centimeter?
Found 2 solutions by jim_thompson5910, harpazo:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Hero's (or Heron's) Formula (Used to Find the Area of a Triangle Given its Three Sides)


In order to find the area of a triangle 'A' with side lengths of 'a', 'b', and 'c', we can use Hero's Formula:



A=sqrt%28S%28S-a%29%28S-b%29%28S-c%29%29 where S is the semiperimeter and it is defined by S=%28a%2Bb%2Bc%29%2F2

Note: "semi" means half. So the semiperimeter is half the perimeter.



So let's first calculate the semiperimeter S:



S=%28a%2Bb%2Bc%29%2F2 Start with the semiperimeter formula.



S=%289%2B7%2B5%29%2F2 Plug in a=9, b=7, and c=5.



S=%2821%29%2F2 Add.



S=10.5 Divide.



----------------------------------------



A=sqrt%28S%28S-a%29%28S-b%29%28S-c%29%29 Now move onto Hero's Formula.



A=sqrt%2810.5%2810.5-9%29%2810.5-7%29%2810.5-5%29%29 Plug in S=10.5, a=9, b=7, and c=5.



A=sqrt%2810.5%281.5%29%283.5%29%285.5%29%29 Subtract.



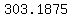A=sqrt%28303.1875%29 Multiply.



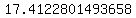A=17.4122801493658 Take the square root of 303.1875 to get 17.4122801493658.



So the area of the triangle with side lengths of a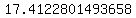=9, b=7, and c=5 is roughly 17.4122801493658 square units.

Answer by harpazo(655) About Me  (Show Source):
You can put this solution on YOUR website!
You need Heron's Formula.
Visit this link:
http://www.mathopenref.com/heronsformula.html