Question 877009: Please help with the following! I've been trying to crack it for days.
Real is investigating the rate of change of the function y=cosx on the interval XE[0,2pi] . He determines the instantaneous rate of change at x=0,pi, and 2pi by inspection and believes that the IROC at the roots of y=cosx could be relevant in determining an equation r(x) to predict the instantaneous rate of change of the function y=cosx on the interval xE[0,2pi] . Find the equation that represents the IROC for y=cosx and use it to determine the exact instantaneous rate of change at x=pi/4.
Thank you in advanced!
Found 2 solutions by richard1234, KMST:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you've been trying to crack this problem for days, you should read over some derivatives of elementary functions.
dy/dx = -sin x
dy/dx at x = pi/4 is -sin(pi/4) = -sqrt(2)/2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  and and  , but how can you show a reasoning for that solution, and what reasoning should you use? , but how can you show a reasoning for that solution, and what reasoning should you use?
Not knowing what level math class the problem came from, and what kind of reasoning appeals to the instructor who made up the problem, I do not see what Real is thinking.
Maybe the students in your math class have been given "memorizable" formulas and tips to calculate derivatives. In that case you would know that the IROC is the derivative and that the derivative of cosine is -sine.
Maybe your class is not into derivatives yet, and this problem is a "warmup" to the concept of derivatives. In that case, you may be expected to calculate the IROC as a limit.
It could also be that you are deep into calculus and Taylor series. In that case, maybe you could use that and Real's belief "that the IROC at the roots of y=cosx could be relevant in determining an equation r(x) to predict the instantaneous rate of change of the function y=cosx on the interval xE[0,2pi] ".
Alternatively, students who never heard of limits or calculus can visualize the IROC as a velocity. THat sound more real than Real.
Talking about velocities, I will make the independent variable  , the time in seconds, and my , the time in seconds, and my  and and  will just indicate the position of a moving point, P. (Sorry, I like speeds and rates of change as function of time, will just indicate the position of a moving point, P. (Sorry, I like speeds and rates of change as function of time,  , and if we are going to visualize something, a small dose of realism helps). , and if we are going to visualize something, a small dose of realism helps).
Then  is the x-coordinate of the shadow on the x-axis of a point circling the origin in the x-y plane at constant speed, and its velocity is is the x-coordinate of the shadow on the x-axis of a point circling the origin in the x-y plane at constant speed, and its velocity is  . .
AS A LIMIT:
For any value of  , the average ROC for the interval , the average ROC for the interval 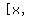 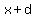 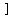 is is

Then 
From there you could prove that  several ways, but you may need to use theorems about limits that were taught in class, like several ways, but you may need to use theorems about limits that were taught in class, like

AS A SHADOW:
A point P starts at position (1,0) in the x-y plane, when  . .
It moves counterclockwise, in a circle centered at the origin.
The radius of that circle is  (in whatever units of length we are using). (in whatever units of length we are using).
The angular velocity pf P is  (in radians per second). (in radians per second).
The position of point P is a vector that is changing direction with time.
Its x-component is  . .
The speed,  of point P is a number and is equal the radius times the angular velocity, so it is also equal to of point P is a number and is equal the radius times the angular velocity, so it is also equal to  (in units of length per second). (in units of length per second).
The velocity of P is a vector that is changing direction with time,
always perpendicular to the radius from the origin to P,
always with a magnitude  . .
Its component in the x-direction given by  . .
Compared to point P, the projection of point P on the x-axis,
has the same x-coordinate,
and the same x-component of velocity.
The IROC of the x-coordinate of P's shadow,
which varies with time  as as  . .
(between  and and  seconds and for as long as we let P move) seconds and for as long as we let P move)
is  . .
I know I name the variables differently, but a function is the same, no matter what you call the variables.
You can change the names of the variables. I don't care what names I'm called and  do not mind if you call them do not mind if you call them  and and  respectively. respectively.
I did not want to use  , because I am more familiar with an x-y plane that with a u-v set of coordinates. , because I am more familiar with an x-y plane that with a u-v set of coordinates.
|
|
|