SOLUTION: If log<sub>a</sub>(m) = p and log<sub>b</sub>(m) = q (a&b are bases) prove that {{{(p-q)/(p+q)}}} = {{{(log((b))-log((a)))/(log((b))+log((a)))}}}

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: If log<sub>a</sub>(m) = p and log<sub>b</sub>(m) = q (a&b are bases) prove that {{{(p-q)/(p+q)}}} = {{{(log((b))-log((a)))/(log((b))+log((a)))}}}      Log On


   

Question 87657: If loga(m) = p and logb(m) = q (a&b are bases)
prove that %28p-q%29%2F%28p%2Bq%29 = %28log%28%28b%29%29-log%28%28a%29%29%29%2F%28log%28%28b%29%29%2Blog%28%28a%29%29%29
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!

If loga(m) = p and logb(m) = q (a&b are bases) 
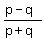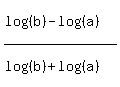prove that %28p-q%29%2F%28p%2Bq%29 = %28log%28%28b%29%29-log%28%28a%29%29%29%2F%28log%28%28b%29%29%2Blog%28%28a%29%29%29

 loga(m) = p   and   logb(m) = q

Rewrite these log equations as exponential equations:

      ap = m              bq = m 

Now take the log10 of both sides.  When the
base is 10 we do not write the base, as it is understood
to be 10 when it is not written:

 log(ap) = log(m)    log(bp) = log(m)

Use the rule of logs that allows you to move the exponent
of what the log is taken of out in friont as a multiplier:

p·log(a) = log(m)      q·log(b) = log(m) 

Solve for p and q:

     log(m)                        log(m)
p = --------                  q = --------
     log(a)                        log(b)

Let's find p - q

         log(m)     log(m)
p - q = -------- - --------  
         log(a)     log(b)

Get LCD = log(a)log(b)

         log(m)log(b)     log(m)log(a)
p - q = -------------- - -------------- 
         log(a)log(b)     log(b)log(a)

         log(m)log(b) - log(m)log(a)
p - q = ---------------------------- 
               log(a)log(b)


=====================================
Similarly, let's find P + q

         log(m)     log(m)
p + q = -------- + --------  
         log(a)     log(b)

         log(m)log(b)     log(m)log(a)
p + q = -------------- + -------------- 
         log(a)log(b)     log(b)log(a)


         log(m)log(b) + (log m)(log a)
p + q = -------------------------------- 
               log(a)log(b)   

==========================================

Now divide p - q by p + q

 p - q     log(m)log(b) - log(m)log(a)     log(m)log(b) + log(m)log(a)
------- = ----------------------------- ÷ -----------------------------
 p + q          log(a)log(b)                      log(a)log(b)


Invert the second fraction and multiply

 p - q     log(m)log(b) - log(m)log(a)           log(a)log(b)
------- = ----------------------------- × -----------------------------
 p + q         log(a)log(b)                log(m)log(b) + log(m)log(a)

Cancel the (log a)(log b)'s
                                                        1
 p - q     log(m)log(b) - log(m)log(a)           log(a)log(b)
------- = ----------------------------- × -----------------------------
 p + q         log(a)log(b)                log(m)log(b) + log(m)log(a)
                      1


 p - q     log(m)log(b) - log(m)log(a)        
------- = ----------------------------- 
 p + q     log(m)log(b) + log(a)log(a)


Factor log(m) out of top and bottom on the right side:

 p - q     log(m)[log(b) - log(a)]        
------- = ------------------------- 
 p + q     log(m)[log(b) + log(a)]

Cancel the (log m)'s

             1
 p - q     log(m)[log(b) - log(a)]        
------- = ------------------------- 
 p + q     log(m)[log(b) + log(a)]
              1 

              
 p - q     log(b) - log(a)        
------- = ----------------- 
 p + q     log(b) + log(a)

Edwin