Question 876239: If a^2,b^2,c^2 are in AP then prove that 1/b+c,1/c+a,1/a+b are also in AP.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a², b², c² are in AP then prove that 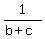 , ,  , , 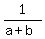 are also in AP. are also in AP.
Since the second part is more complicated than the first part, we
begin by proving the converse, and then we hope we can reverse the
steps to prove the original.
So first we try to prove the converse:
If 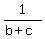 , ,  , , 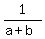 are in AP, then a², b², c² are also in AP.
Three terms are in AP, if and only if are in AP, then a², b², c² are also in AP.
Three terms are in AP, if and only if
 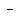    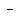 
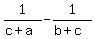  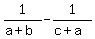
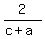  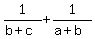 Multiply through by the LCD of (c+a)(b+c)(a+b) assuming that LCD is not 0.
2(b+c)(a+b) = 1(c+a)(a+b) + 1(c+a)(b+c)
2(ba+b²+ca+cb) = (ca+cb+a²+ab) + (cb+c²+ab+ac)
2ba+2b²+2ca+2cb = ca+cb+a²+ab+cb+c²+ab+ac
Write product of letters in alphabetical order so we can
easily identify like terms:
2ab+2b²+2ac+2bc = ac+bc+a²+ab+bc+c²+ab+ac
2ab+2b²+2ac+2bc = 2ac+2bc+a²+2ab+c²
Subtract 2ab+2ac+2bc from both sides:
2b² = a²+c²
Write 2b² as b²+b²
b²+b² = a²+c²
b²-a² = c²-b²
Therefore a²,b²,c² are in AP because
Three terms are in AP, if and only if
Multiply through by the LCD of (c+a)(b+c)(a+b) assuming that LCD is not 0.
2(b+c)(a+b) = 1(c+a)(a+b) + 1(c+a)(b+c)
2(ba+b²+ca+cb) = (ca+cb+a²+ab) + (cb+c²+ab+ac)
2ba+2b²+2ca+2cb = ca+cb+a²+ab+cb+c²+ab+ac
Write product of letters in alphabetical order so we can
easily identify like terms:
2ab+2b²+2ac+2bc = ac+bc+a²+ab+bc+c²+ab+ac
2ab+2b²+2ac+2bc = 2ac+2bc+a²+2ab+c²
Subtract 2ab+2ac+2bc from both sides:
2b² = a²+c²
Write 2b² as b²+b²
b²+b² = a²+c²
b²-a² = c²-b²
Therefore a²,b²,c² are in AP because
Three terms are in AP, if and only if
       Now we must reverse the steps to prove the original theorem.
We have only proved the converse.
We now assume that we are given that a²,b²,c² are in AP. So
b²-a² = c²-b²
b²+b² = a²+c²
2b² = a²+c²
Add 2ab+2ac+2bc to both sides:
2ab+2b²+2ac+2bc = 2ac+2bc+a²+2ab+c²
Write 2ac as ac+ac, 2bc as bc+bc, 2ab as ab+ab
2ab+2b²+2ac+2bc = ac+ac+bc+bc+a²+ab+ab+c²
Rearrange the terms on the right:
2ab+2b²+2ac+2bc = ac+bc+a²+ab+bc+c²+ab+ac
Rewrite some of the terms by changing the order
of factors:
2ba+2b²+2ca+2cb = ca+cb+a²+ab+cb+c²+ab+ac
Factor 2 out of the left side and group the terms on the right:
2(ba+b²+ca+cb) = (ca+cb+a²+ab) + (cb+c²+ab+ac)
Factor each expression in parentheses by grouping:
2[(ba+b²)+(ca+cb)] = [(ca+cb)+(a²+ab)] + [(cb+c²)+(ab+ac)]
2[b(a+b)+c(a+b)] = [c(a+b)+a(a+b)] + [c(b+c)+a(b+c)]
2(b+c)(a+b) = (c+a)(a+b) + (c+a)(b+c)
Divide through by (c+a)(b+c)(a+b) assuming that it is not 0.
Now we must reverse the steps to prove the original theorem.
We have only proved the converse.
We now assume that we are given that a²,b²,c² are in AP. So
b²-a² = c²-b²
b²+b² = a²+c²
2b² = a²+c²
Add 2ab+2ac+2bc to both sides:
2ab+2b²+2ac+2bc = 2ac+2bc+a²+2ab+c²
Write 2ac as ac+ac, 2bc as bc+bc, 2ab as ab+ab
2ab+2b²+2ac+2bc = ac+ac+bc+bc+a²+ab+ab+c²
Rearrange the terms on the right:
2ab+2b²+2ac+2bc = ac+bc+a²+ab+bc+c²+ab+ac
Rewrite some of the terms by changing the order
of factors:
2ba+2b²+2ca+2cb = ca+cb+a²+ab+cb+c²+ab+ac
Factor 2 out of the left side and group the terms on the right:
2(ba+b²+ca+cb) = (ca+cb+a²+ab) + (cb+c²+ab+ac)
Factor each expression in parentheses by grouping:
2[(ba+b²)+(ca+cb)] = [(ca+cb)+(a²+ab)] + [(cb+c²)+(ab+ac)]
2[b(a+b)+c(a+b)] = [c(a+b)+a(a+b)] + [c(b+c)+a(b+c)]
2(b+c)(a+b) = (c+a)(a+b) + (c+a)(b+c)
Divide through by (c+a)(b+c)(a+b) assuming that it is not 0.
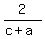  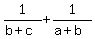 Write
Write 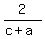 as as   
 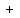   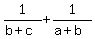 Rearranging the terms:
Rearranging the terms:
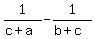  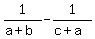 Therefore
Therefore
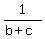 , ,  , , 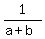 are in AP, because
three terms are in AP, if and only if are in AP, because
three terms are in AP, if and only if
       Edwin
Edwin
|
|
|