Question 875547: Im stuck, please help me solve and go into detail
Find the exact value
Given that sin Ө = -4/5 with Ө in quadrant IV, find tan 2Ө
Found 2 solutions by lwsshak3, KMST:
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the exact value
Given that sin Ө = -4/5 with Ө in quadrant IV, find tan 2Ө
***
you are working with a (3-4-5) reference right triangle in quadrant IV
sin Ө=-4/5 (given)
cos Ө=3/5
sin 2Ө=2sinӨcosӨ=2*-4/5*3/5=-24/25
cos 2Ө=cos^2Ө-sin^2Ө=9/25-16/25=-7/25
tan 2Ө-sin 2Ө/cos 2Ө=24/7
..
Check:
sin Ө=-4/5
Ө≈306.87˚
2Ө≈613.74˚
tan 2Ө≈3.4286…
exact value as calculated=24/7≈3.4287…
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! With  in quadrant IV, cosine will be positive, while sine and tangent are negative. in quadrant IV, cosine will be positive, while sine and tangent are negative.
That information, along with the value of one of the trigonometric functions allows you to calculate all trigonometric function values for  , ,
and using trigonometric identities, you can calculate values for 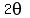 too. too.
The angle  could be the angle AOP shown below, measuring about {{-53^o}}} . could be the angle AOP shown below, measuring about {{-53^o}}} .
 I could make I could make  going from A to P the other way around, going from A to P the other way around,
but if I say that  , ,
or if I say  , ,
or even  , ,
the trigonometric functions of those angles are all the same,
because they all have OA and OP for sides.
 is the y-coordinate of point P is the y-coordinate of point P
 is the x-coordinate of point P is the x-coordinate of point P
We know that the squares of sine and cosine add up to 1, so




So  , and , and 
From there, you could
A) calculate  , ,
and then apply the trigonometric identity

So 
B) or calculate 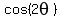 and and 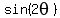 using the trigonometric identities below, using the trigonometric identities below,
and then divide sine by cosine to get tangent
 and and

|
|
|