Question 875341: find the x-intercept and y-intercept, the foci, the center and circle whether the following equation has a horizonatl or vertical axis:
x^2/100 +y^2/36 =1
Please help with this!1 Thanks :)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  <----> <----> 
Since  appears only as its square, appears only as its square,
substituting 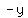 for for  gives us the same equation, meaning that the curve is symmetrical to both sides (above and below) the x-axis. gives us the same equation, meaning that the curve is symmetrical to both sides (above and below) the x-axis.
So, the x-axis is a  axis of symmetry of the curve axis of symmetry of the curve
Since  appears only as its square, appears only as its square,
substituting  for for  gives us the same equation, meaning that the curve is symmetrical to both sides (left and right)of the y-axis. gives us the same equation, meaning that the curve is symmetrical to both sides (left and right)of the y-axis.
So, the y-axis is a  axis of symmetry of the curve. axis of symmetry of the curve.
The x-intercepts, are the points on the x-axis, where  , ,
and  --> --> --> --> --> --> . .
So the x-intercepts are the points (-10,0) and (10,0).
The y-intercepts, are the points on the y-axis, where  , ,
and  --> --> --> --> --> --> . .
So the y-intercepts are the points (0,-6) and (0,6).
With the x- and y-axes as axes of symmetry, we get the idea that the curve has the origin as its center.
GENERAL INFORMATION:
The equation  is the equation of an ellipse, is the equation of an ellipse,
centered at the origin, with the x- and y-axes for axes of symmetry.
If we make  it turns into s circle with radius it turns into s circle with radius : :
 <---> <---> <---> <---> , ,
but is 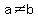 it will be stretched (horizontally or vertically) into an ellipse. it will be stretched (horizontally or vertically) into an ellipse.
The ellipse span along the x-axis measures  (with extreme points at (-a,0) and (a,0)), (with extreme points at (-a,0) and (a,0)),
and along the y-axis the ellipse measures 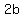 (with extreme points at (0,-b) and (0,b)). (with extreme points at (0,-b) and (0,b)).
In the case of  <----> <---->  , ,
the horizontal span of the ellipse, from (-10,0) to (10,0),
with length  , is longer than the vertical span, from(0,-6) to (0,6), , is longer than the vertical span, from(0,-6) to (0,6),
so the portion of the horizontal axis connecting vertices (-10,0) and (10,0) is called the major axis.
The segment of the vertical axis ending in (0,-6) and (0,6) is called the minor axis, and its ends may be called co-vertices of the ellipse.

The distance from center to the vertices  is called the semi-major axis, is called the semi-major axis,
and the distance from center to the co-vertices  is called the semi-minor axis. is called the semi-minor axis.
The foci are at a distance  from the center of the ellipse, and from the center of the ellipse, and
 . .
So, in this case, 



So, the focal distance is  --> -->  , ,
and the foci are at that distance from the center, along the major axis.
That means that the foci are the points (-8,0) and (8,0).

|
|
|