Question 875156: PLEASE HELP. WHAT IS THE EQUATION OF A LINE THROUGH (4, -1) AND WHOSE SEGMENT INTERCEPTED BETWEEN THE AXES IN THE 4TH QUADRANT IS EQUAL TO 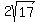 . THANKS IN ADVANCE. . THANKS IN ADVANCE.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAIMER:
The solution that follows is not elegant.
I would welcome any alternative.
If this strategy was the expected one, and maybe there is no better way, I would love to know that too.
The situation in the problem is illustrated in the drawing below.
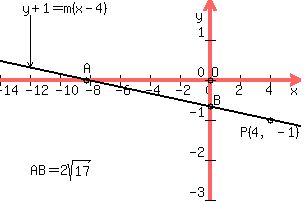 We are looking for We are looking for  and the coordinates of and the coordinates of 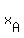 and and 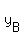 of A and B, of A and B,
and all of them should be negative.
We use  <---> <---> to find to find 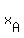 and and 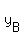 as a function of as a function of  . .
 ---> --->  ---> ---> 
 ---> --->  ---> ---> 
Since  <--> <--> <--> <-->
and  , ,

Substituting  and and  we get we get








There are 4 real solutions to that equation, and we can find their approximate values. I suppose that using a graphing calculator was expected, but I used the computer, since I am already using it to access the answer this question.
The solution we are interested in is the one with
 , ,
because that would give us  . .
That solution is  , ,
which makes  , ,
so the equation of the line is

|
|
|