Question 874948: how to find the area of the triangle whose sides are 32m, 38m, and 45m?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is usually more than one way to solve a problem, and in this case, I immediately think of two ways. If this is a homework problem, you would want to use the one your teacher expects, based on what you have been taught in class.
Otherwise, you would use the one that is most efficient for you.
USING HERON'S FORMULA:
Heron's formula can be written in many ways.
Here is one of them.
If the lengths of the sides of a triangle (in whatever units) are
 , ,  , and , and  , ,
and we define the semi-perimeter as
 , ,
then the area of the triangle (in whatever units squared) can be calculated as
 . .
In your case, the lengths in meters are
 , ,  , ,  , and , and
 . .
So the area, in square meters can be calculated as either
 , ,
or  . .
Either way, that is approximately  . .
If we wanted an exact expression,
 is the most elegant way to write it. is the most elegant way to write it.
USING LAW OF COSINES:
With two sides, and the sine of the angle in between,
we can calculate the area.
Having the length of all 3 sides,
 , ,  , and , and  , ,
the law of cosines allows us to calculate the measure of any one of the angles.
With two sides, and the angle in between,
If we wanted to calculate the measure of  , ,
the angle opposite side  and between the other two sides, and between the other two sides,
we would use

Substituting the values for  , ,  , and , and  , we get , we get






 (simplifying). (simplifying).
We do not need to calculate  , ,
because we can calculate 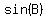 directly from directly from 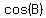 as as


So we can calculate the area of the triangle as

As an approximate value, that is approximately  . .
|
|
|