SOLUTION: PLEASE HELP. SHOW THAT THE LINES {{{ X - Y - 8 = 0 }}} , {{{ 3X + 2Y + 1 = 0 }}} , {{{ X - Y - 3 = 0 }}} AND {{{ 2X + 3Y + 24 = 0 }}} ARE THE SIDES OF AN ISOSCELES TRAPEZOID AND FI

Algebra ->  Test -> SOLUTION: PLEASE HELP. SHOW THAT THE LINES {{{ X - Y - 8 = 0 }}} , {{{ 3X + 2Y + 1 = 0 }}} , {{{ X - Y - 3 = 0 }}} AND {{{ 2X + 3Y + 24 = 0 }}} ARE THE SIDES OF AN ISOSCELES TRAPEZOID AND FI      Log On


   

Question 874920: PLEASE HELP. SHOW THAT THE LINES +X+-+Y+-+8+=+0+ , +3X+%2B+2Y+%2B+1+=+0+ , +X+-+Y+-+3+=+0+ AND +2X+%2B+3Y+%2B+24+=+0+ ARE THE SIDES OF AN ISOSCELES TRAPEZOID AND FIND ITS AREA.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Since system%28red%28x-y-8=0%29%2Cgreen%28x-t-3=0%29%29 has no solution,
the lines red%28x-y-8=0%29 and green%28x-y-3=0%29 are parallel.
What's more, the slope of the lines is 1 ,
since red%28x-y-8=0%29 --> red%28y=x-8%29
and green%28x-y-3=0%29 --> green%28y=x-3%29 .
The slope of the lines is 1 .
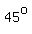Since tan%2845%5Eo%29=1 , the lines make a 45%5Eo with the positive x-axis.
The bases are part of those parallel lines, which make a 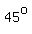45%5Eo with the positive x-axis.
A perpendicular to those lines from the y-intercept of green%28y=x-3%29 at (0,-3} forms an isosceles right triangle with red%28y=x-8%29 and the y-axis, with a hypotenuse of 8-3=5. So the length of the legs of that triangle is
5sin%2845%5Eo%29=5sqrt%282%29%2F2 , and that is the distance between the lines and the height of the trapezoid.


The vertices of the trapezoid can be calculated as the intersections of the lines.
system%28red%28y=x-8%29%2C3x%2B2y%2B1=0%29 --> system%28x=3%2Cy=-5%29
system%28red%28y=x-8%29%2C2x%2B3y%2B24=0%29 --> system%28x=0%2Cy=-8%29
system%28green%28y=x-3%29%2C3x%2B2y%2B1=0%29 --> system%28x=1%2Cy=-2%29
system%28green%28y=x-3%29%2C2x%2B3y%2B24=0%29 --> system%28x=-3%2Cy=-6%29
The vertices are (3,-5) and (0,-8) for the base on red%28y=x-8%29
The vertices are (1,-2) and (-3,-6) for the base on green%28y=x-3%29
The length of the bases is the distance between their vertices, so those lengths are
sqrt%28%283-0%29%5E2%2B%28-5%2B8%29%5E2%29=sqrt%289%2B9%29=sqrt%282%2A9%29=3sqrt%282%29
and sqrt%28%281%2B3%29%5E2%2B%28-2%2B6%29%5E2%29=sqrt%2816%2B16%29=sqrt%282%2A16%29=4sqrt%282%29

The area of a trapezoid (isosceles or not) can be calculated as
In+this+case+the+area+is%0D%0A%281%2F2%29%28base%5B1%5D%2Bbase%5B2%5D%29%28height%29

and in close-up

To prove that it is an isosceles trapezoid, we could easily prove that the non-parallel sides (the legs) are congruent.
The length of one of those sides is the distance between vertices on 2x%2B3y%2B24=0 , (0,-8) and(-3,-6).
That distance is
sqrt%28%280%2B3%29%5E2%2B%28-8%2B6%29%5E2%29=sqrt%289%2B4%29=sqrt%2813%29 .
The length of the other leg is the distance between vertices on
3x%2B2y%2B1=0%29 , (1,-2) and (3,-5).
That distance is
sqrt%28%281-3%29%5E2%2B%28-2%2B5%29%5E2%29=sqrt%284%2B9%29=sqrt%2813%29 .