SOLUTION: I need to find the equation of a hyperbola with foci at (-3,7) and (-3,-5) whose transverse axis is 8 units long. I have no idea where to even start with this, but I have graphed t

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: I need to find the equation of a hyperbola with foci at (-3,7) and (-3,-5) whose transverse axis is 8 units long. I have no idea where to even start with this, but I have graphed t      Log On


   

Question 874663: I need to find the equation of a hyperbola with foci at (-3,7) and (-3,-5) whose transverse axis is 8 units long. I have no idea where to even start with this, but I have graphed the points given.
Found 2 solutions by KMST, josgarithmetic:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
We realize that both foci have x=-3 .
That means that the center, foci and vertices have x=-3 ,
and that the transverse axis, connecting the vertices is part of the vertical line x=-3 .
The distance between the foci is the difference in their y-coordinates,
7-%28-5%29=7%2B5=12 .
The center is midway between the foci.
The distance between each focus and the center is the focal distance,
c=12%2F2=highlight%286%29
The center is the midpoint of the segment connecting the foci,
so its coordinates are averages of the foci's coordinates:
x=%28-3%2B%28-3%29%29%2F2=highlight%28-3%29 and y=%287%2B%28-5%29%29%2F2=%287-5%29%2F2=2%2F2=highlight%281%29
So the center is at (-3,1).
That means that 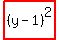%28x-%28-3%29%29%5E2=highlight%28%28x%2B3%29%5E2%29 and highlight%28%28y-1%29%5E2%29 appear in the equation of the hyperbola.

Since the distance between the vertices is 8 , the length of the transverse axis,
each vertex is a=8%2F2=highlight%284%29 units away (above and below) the center.
Their y coordinates of the vertices are highlight%284%29 units away from the y=1 of the center,
abs%28y-1%29=4 ,
and for the other points on the hyperbola,
the y coordinates are farther away from the y=1 of the center.
So abs%28y-1%29%3E=4<-->%28y-1%29%5E2%3E=4%5E2<-->%28y-1%29%5E2%2F4%5E2%3E=1 .
The equation will be
%28y-1%29%5E2%2F4%5E2-%28x%2B3%29%5E2%2Fb%5E2=1<--->%28y-1%29%5E2%2F16-%28x%2B3%29%5E2%2Fb%5E2=1 . .
The way to find b%5E2 is through the relationship c%5E2=a%5E2%2Bb%5E2 .
Substituting the known values a=3 and c=6
6%5E2=4%5E2%2Bb%5E2-->36=16%2Bb%5E2-->36-16=b%5E2-->highlight%28b%5E2=20%29
Substituting that value, the equation is
highlight%28%28y-1%29%5E2%2F16-%28x%2B3%29%5E2%2F20=1%29 .

Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Transverse Axis is the segment connecting the vertices. Yours is a length of 8 units, so a=4. Distance from center to either vertex is 4 units, half of the transverse axis length.

Focal length: %287%2Babs%28-5%29%29%2F2=6=c. Again using focus information, the center, y value is the average of the focus y values: %287%2B%28-5%29%29%2F2=1.
The center is (-3,1).

The negative sign is on the term for x, since your foci are vertically arranged. If the hyperbola were standard position, vertices would be on the y axis. In your case, center is NOT at the origin.

Now you have center, a, and c. You can say,
highlight_green%28%28y-1%29%5E2%2F4%5E2-%28x%2B3%29%5E2%2Fb%5E2=1%29.
You still want the b value.

A substitution is often used in deriving the equation of a hyperbola.
The effect is the relationship a%5E2%2Bb%5E2=c%5E2
b%5E2=c%5E2-a%5E2.
You example has b%5E2=6%5E2-4%5E2=36-16=20.

Finally, your standard form hyperbola is highlight%28%28y-1%29%5E2%2F4%5E2-%28x%2B3%29%5E2%2F20=1%29