Question 874471: please help me prove identity for cos^4x+sin^4x=(1/4)cos4x+(3/4)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The trickiest part of this problem requires a good understanding of how the identities can be used. As you can see, the arguments of the Trig functions are x's on the left side and 4x on the right side. So at some point we will need to change the arguments to match. Changing arguments requires identities.
There are no "Quadruple angle" or "Quarter angle" identities so we cannot just go directly from x to 4x (or vice versa). But we do have Double angle and Half angle identities. By using them twice we can change x to 4x.
The tricky part is understanding that both Double angle and Half angle identities can be used! For example
sin(2x) = 2sin(x)cos(x)
As you can see the argument on the left is twice the arguments on the right. So if we have en expression which matches the pattern of the right side, then we can use it to double the arguments by replacing the expression with the left side. For example:
2sin(5x)cos(5x)
matches the pattern of the right side. So we can replace it with the corresponding left side:
sin(2(5x)) or just sin(10x), doubling the arguments!
The Half angle identities can also be used, despite their names! For example,
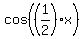 = + = +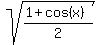
The argument on the right is twice the argument on the left. So if we have an expression matching the pattern of the left side, we can replace it with the corresponding right side, doubling the argument! We will be using Half angle identities to solve this problem.
[Note: algebra.com has some issues with plus or minus signs. However, with the squaring that you will see, they become unnecessary. So I will not be using them below.]

First we will rewrite the left side as squares of a square:

Rewriting cos(x) and sin(x) so they fit the pattern of the left side of the Half angle formulas:

Replacing them with the corresponding right sides of the identities (w/o the plus or minus):

Squaring the square roots:

Before using the Half angle identities again to get the arguments up to 4x, we will do some simplifying. First I'll factor out (1/2)^2:

Squaring the squares:

Adding like terms:

Now we will use the Half angle formula:


Squaring the square root:

Simplifying...


Distributing the 1/4:

Commutative Property:

|
|
|