Question 874131: In a five mile race betty was 1/4 of a mile back when Ann crossed the finish line and Cindy was 1/3 of a mile back when Betty finished. Assuming that all three maintained their same pace throughout the race how far back was Cindy when Ann finished the race?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ONE WAY TO DO IT:
In the time that Ann ran  miles, miles,
Betty only covered  miles. miles.
Betty is slower than Ann.
Compared to Ann's speed, Betty's speed is
 of Ann's speed. of Ann's speed.
Betty's speed is 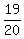 of Ann's speed. of Ann's speed.
In the time that Betty ran  miles, miles,
Cindy only covered  miles. miles.
Cindy is slower than Betty .
Compared to Betty's speed, Cindy's speed is
 of Betty's speed. of Betty's speed.
Cindy's speed is 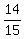 of Betty's speed. of Betty's speed.
Compared to Ann's speed, Cindy's speed is
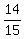 of of 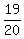 of Ann's speed, or of Ann's speed, or
 of Ann's speed. of Ann's speed.
So, in the time that Ann ran  miles, miles,
Cindy covered  miles. miles.
That means that when Ann finished the race,
Cindy had only ran 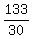 out of the out of the  miles. miles.
So Cindy was
 miles back. miles back.
ANOTHER WAY:
We could say that Ann ran the 5 miles in  minutes, and then we can calculate Ann's, Betty's and Cindy"s speeds in miles per minute based on that: minutes, and then we can calculate Ann's, Betty's and Cindy"s speeds in miles per minute based on that:
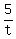 = Ann's speed. = Ann's speed.
Since Betty was  mile back, mile back,
and had only covered 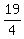 miles in that time miles in that time  , ,
 = Betty's speed. = Betty's speed.
So Betty would take  minutes to finish. minutes to finish.
In that time, Cindy had only ran  miles, miles,
so Cindy's speed, in miles per minute, is
 . .
That means that, in the time  that it took for Ann to finish the race, that it took for Ann to finish the race,
Cindy had covered  miles. miles.
So, to get to the finish line, Cindy still had to run
 miles back. miles back.
SIMPLER:
We can set an arbitrary time.
Let's say that Ann's time was 40 minutes.
Ann ran at  miles per minute. miles per minute.
Betty had ran  miles in those 40 minutes. miles in those 40 minutes.
Betty ran at  miles per minute. miles per minute.
At that speed it would take her
 minutes to finish the 5 mile race. minutes to finish the 5 mile race.
In that time, Cindy had only run  miles. miles.
Cindy's speed was about  miles per minute. miles per minute.
At that speed, in the 40 minutes that it took Ann to finish the race,
Cindy covered approximately  miles, miles,
and at that point she was about
 miles back. miles back.
|
|
|