Question 873914: The sum of the digits of a two-digit numeral is 10. The number named by the numeral is 18 more than the number named when the digits are reversed. What is the original numeral?
Equation & answer please.. Thank You!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = tens digit. = tens digit.
 = ones/units digit. = ones/units digit.
One of the statements in the problem says that 
 = value of the two-digit numeral. = value of the two-digit numeral.
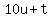 = value of the number named when the digits are reversed. = value of the number named when the digits are reversed.
Another statement in the problem says that
 is is  more than more than 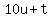 . .
That can be written as the equation
 . .
Subtracting  and and  from both sides we get from both sides we get
 , which simplifies to , which simplifies to

Then, dividing both sides by  , we get , we get
 ---> ---> ---> --->
Take the equation above, and  written at the beginning, written at the beginning,
we have the system  , ,
which we call "a system of linear equations."
We can solve it "by substitution,"
meaning that we take an expression that is equal to one variable from one equation,
and substitute that expression for the variable in the other equation.
Substituting 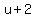 for for  in in  , we get , we get
 --> --> --> --> --> --> --> --> --> --> --> -->
Now, we substitute the value found for  in in  to find the value of to find the value of  : :
 --> --> --> --> . .
So, with  and and  , the two-digit numeral is , the two-digit numeral is  . .
|
|
|