|
Question 873017: A bridge is built in the shape of a parabolic arch. The beidge has a span of 120 feet and a maximum height of 25 feet. If the vertex of the parabola is located at (0,0), find the height of the arch 50 feet from the center.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bridge is built in the shape of a parabolic arch.
The beidge has a span of 120 feet and a maximum height of 25 feet.
If the vertex of the parabola is located at (0,0), find the height of the arch 50 feet from the center.
:
First find the equation for the parabola, using the ax^2 + bx + c = y
It crosses the y axis at the origin so we can ignore c
A 120 ft span, +/-60 on the graph
Find the equation for each pair
x=-60, y =-25
-60^2a - 60b = -25
3600a - 60b = -25
and
x=+60, y =-25
3600a + 60b = -25, add to the 1st equation
3600a - 60b = -25
-------------------Adding eliminates b find a
7200a = -50
a = -50/7200
a = -.00694
;
We know b is 0 because the vertex is at the origin
a simple equation
y = -.00694x^2
looks like this
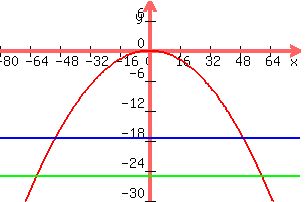
Surface is green
:
find the height of the arch 50 feet from the center.
x=50
-.00694(50^2) = -17.5, height will be 25-17.5 = 7.5m above the surface (purple)
|
|
|
| |