Question 872245: in your pocket you have a quarters, two dimes, and three pennies. If all amounts are equally likely, what is the probability that you can match the"change" part of your bill? ( If the bill were $7.10, thw change part would be the $0.10.)
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website!
We can choose the number of quarters to use 2 ways,
that is, we can choose to use no quarters, or 1 quarter.
That's 2 ways.
For each of those 2 choices for the number of quarters,
we can choose the number of dimes to use 3 ways,
that is, we can choose to use no dimes, 1 dime, or 2 dimes.
So we can choose the numbers of quarters and dimes to use
in 2×3 or 6 ways.
For each of those 2×3 or 6 choices for the number of quarters
and dimes to use, we can choose the number of pennies 4 ways,
that is, we can choose to use no pennies, 1 penny, 2 pennies,
or 3 pennies. So we can choose the numbers of quarters, dimes
and pennies to use in 2×3×4 or 24 ways.
No two of those 24 combinations of coins will produce the same
number of cents, so there are 24 possible numbers of cents
we can make with 1 quarter, 2 dimes and 3 pennies.
There are 100 different numbers of cents our bill can have,
.00, .01, ... .99
So the probability that we can match the "change" part of
our bill is  or 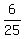 . [ 24% of the time
we can match the "change" and 76% of the time we can't].
Edwin
|
|
|
