Question 871692: A pair of fair dice is rolled once. Suppose that you lose $9 if the dice sum to 10 and win $12 if the dice sum to 3 or 2. How much should you win or lose if any other number turns up in order for the game to be fair?
To keep the game for, you should win or lose how much money, if the dice sum to any other number.
(Do not round until the final answer.Then round to the nearest cent as needed.)
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
<
P(1 or 2) = P(green roll) = 3 ways out of 36 = 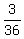 = =  P(10) = P(red roll) = 3 ways out of 36 =
P(10) = P(red roll) = 3 ways out of 36 = 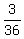 = =  P(any other roll) = P(purple roll) = 31 ways out of 36 =
P(any other roll) = P(purple roll) = 31 ways out of 36 = 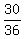 = =  Roll Probability Winning (+) Expectation
or loss (-)
(X) P(X) W(X) P(X)*W(X)
----------------------------------------------
green 1/12 +$12 $1
red 1/12 -$9 -$3/4
purple 5/6 $w $5/6w
----------------------------------------------
Total expectation = $1/4 + 5/6w
For the game to be fair, the total expectation must be 0.
1/4 + 5/6w = 0
5/6w = -1/4
Multiply both sides by 12
10w = -3
w = -3/10 = -$.30
You should lose 30 cents if you get a purple roll.
Edwin
Roll Probability Winning (+) Expectation
or loss (-)
(X) P(X) W(X) P(X)*W(X)
----------------------------------------------
green 1/12 +$12 $1
red 1/12 -$9 -$3/4
purple 5/6 $w $5/6w
----------------------------------------------
Total expectation = $1/4 + 5/6w
For the game to be fair, the total expectation must be 0.
1/4 + 5/6w = 0
5/6w = -1/4
Multiply both sides by 12
10w = -3
w = -3/10 = -$.30
You should lose 30 cents if you get a purple roll.
Edwin
Answer by AnlytcPhil(1807)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question 871692
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
<
P(1 or 2) = P(green roll) = 3 ways out of 36 = 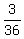 = =  P(10) = P(red roll) = 3 ways out of 36 =
P(10) = P(red roll) = 3 ways out of 36 = 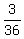 = =  P(any other roll) = P(purple roll) = 31 ways out of 36 =
P(any other roll) = P(purple roll) = 31 ways out of 36 = 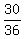 = =  Roll Probability Winning (+) Expectation
or loss (-)
(X) P(X) W(X) P(X)*W(X)
----------------------------------------------
green 1/12 +$12 $1
red 1/12 -$9 -$3/4
purple 5/6 $w $5/6w
----------------------------------------------
Total expectation = $1/4 + 5/6w
For the game to be fair, the total expectation must be 0.
1/4 + 5/6w = 0
5/6w = -1/4
Multiply both sides by 12
10w = -3
w = -3/10 = -$.30
You should lose 30 cents if you get a purple roll.
Edwin
Roll Probability Winning (+) Expectation
or loss (-)
(X) P(X) W(X) P(X)*W(X)
----------------------------------------------
green 1/12 +$12 $1
red 1/12 -$9 -$3/4
purple 5/6 $w $5/6w
----------------------------------------------
Total expectation = $1/4 + 5/6w
For the game to be fair, the total expectation must be 0.
1/4 + 5/6w = 0
5/6w = -1/4
Multiply both sides by 12
10w = -3
w = -3/10 = -$.30
You should lose 30 cents if you get a purple roll.
Edwin
|
|
|