To be divisible by both 2 and 3, it must be a number of the form
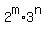 (since it needs no other prime factors to be as small as possible.)
(since it needs no other prime factors to be as small as possible.)
When divided by two, the result is a perfect square:
So 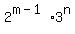 is a perfect square.
Therefore m-1 and n are both even
Therefore m is odd and n is even.
is a perfect square.
Therefore m-1 and n are both even
Therefore m is odd and n is even.
When divided by three, the result is a perfect cube.
So 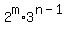 is a perfect cube.
Therefore m and n-1 are both multiples of 3.
Therefore m is a multiple of 3 and m is 1 more than a multiple of 3.
Putting everything together:
m is an odd multiple of 3.
The smallest such positive integer is 3, so m=3
n is even and 1 more than a multiple of 3.
The smallest such positive integer is 4, so n=4.
is a perfect cube.
Therefore m and n-1 are both multiples of 3.
Therefore m is a multiple of 3 and m is 1 more than a multiple of 3.
Putting everything together:
m is an odd multiple of 3.
The smallest such positive integer is 3, so m=3
n is even and 1 more than a multiple of 3.
The smallest such positive integer is 4, so n=4.
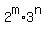



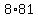

 So there are 648 guests.
Checking:
648÷2 = 324 = 18²
648÷3 = 216 = 6³
Edwin
So there are 648 guests.
Checking:
648÷2 = 324 = 18²
648÷3 = 216 = 6³
Edwin