Question 87108: This is a long one I know, can someone please help me with this one?
Use the arithmetic sequence of numbers 2, 4, 6, 8, 10… to find the following:
a) What is d, the difference between any two consecutive terms?
Answer:
b) Using the formula for the nth term of an arithmetic sequence, what is 101st term? Answer:
c) Using the formula for the sum of an arithmetic sequence, what is the sum of the first 20 terms?
Answer:
d) Using the formula for the sum of an arithmetic sequence, what is the sum of the first 30 terms?
Answer:
e) What observation can you make about the successive partial sums of this sequence (HINT: It would be beneficial to find a few more sums like the sum of the first 2, then the first 3, etc.)?
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! a)
The difference is the factor between each term. So going from 2 to 4, 4 to 6, 6 to 8, and 8 to 10 you see that its adding 2 each time. To verify, pick one term and subtract the previous term from it. So lets say I choose 10: I'm going to subtract 8 from it (which is the previous term) to get a difference of 2. If I pick 8, and subtract 6, I get a difference of 2.
So the difference is: d=2
b)
Using what we found earlier, I know that the sequence counts up by 2 each term. So if I'm at 2 (the 1st term) and I go to 4, this means I increase by 2 each term. If I let n=0 then the term is 2, and if I let n=1 then the term is 4. This basically tells me that the arithmetic sequence is 2n+2. To verify, simply plug in the 1st term (n=0) and you'll get 2. Plug in the 2nd term (n=1) you'll get 4, if I let n=2 I get 6, etc. If I wanted to know the 101st term, let n=100 (remember zero is the first term) and it comes to
 So the 101st term is 202
c)Now lets find the sum of the first 20 terms
Using the sum of arithmetic series formula:
 a[1]=first term, a[n]=nth term (ending term which is the 20th term), and n is the number of terms
Since we know the first term is 2, we know that  .
So lets calculate the 20th term.
Let n=19(remember we started at n=0)
So the term 
Now lets evaluate the sum
 Plug in values.
 Simplify
 So the sum of the first 20 terms is 420.
d)Now lets find the sum of the first 30 terms
Using the sum of arithmetic series formula:
a[1]=first term, a[n]=nth term (ending term which is the 30th term), and n is the number of terms
Since we know the first term is 2, we know that .
So lets calculate the 30th term.
Let n=29(remember we started at n=0)
So the term 
Now lets evaluate the sum
 Plug in values.
 Simplify
 So the sum of the first 30 terms is 930.
e)
Sum of the first 2 terms
2+4=6
Sum of the first 3 terms
2+4+6=12
Sum of the first 4 terms
2+4+6+8=20
Sum of the first 5 terms
2+4+6+8+10=30
Sum of the first 6 terms
2+4+6+8+10+12=42
Sum of the first 7 terms
2+4+6+8+10+12+14=56
Sum of the first 8 terms
2+4+6+8+10+12+14+16=72
Sum of the first 9 terms
2+4+6+8+10+12+14+16+18=90
Sum of the first 10 terms
2+4+6+8+10+12+14+16+18+20=110
Notice how the first sum (which is 6) can be factored like this:
6=2*3
Notice how the second sum (which is 12) can be factored like this:
12=3*4
Notice how the third sum (which is 20) can be factored like this:
20=4*5
Notice how the fourth sum (which is 30) can be factored like this:
30=5*6
Notice how the fifth sum (which is 42) can be factored like this:
42=6*7
Notice how the sixth sum (which is 56) can be factored like this:
56=7*8
Notice how the seventh sum (which is 72) can be factored like this:
72=8*9
Notice how the eighth sum (which is 90) can be factored like this:
90=9*10
Notice how the ninth sum (which is 110) can be factored like this:
110=10*11
and this pattern continues...
Basically, every sum of this sequence can be factored into two numbers in which the second number is one more than the first number
So each sum follows the sequence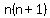 
Notice if we let  we get
which is one of our sums.
Notice if we let  we get
which is also one of the sums
So this helps verify our sequence
|
|
|
