SOLUTION: Find the solutions in the interval [0, 2pi) 2 cos 3x = 1 This is due tomorrow and I am very confused, any and all help is greatly appreciated :)

Algebra ->  Trigonometry-basics -> SOLUTION: Find the solutions in the interval [0, 2pi) 2 cos 3x = 1 This is due tomorrow and I am very confused, any and all help is greatly appreciated :)      Log On


   

Question 871008: Find the solutions in the interval [0, 2pi)
2 cos 3x = 1
This is due tomorrow and I am very confused, any and all help is greatly appreciated :)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
2cos%283x%29=1
cos%283x%29=1%2F2
The cosine function takes all the positive values between 0 and 1, without repeating in quadrant I and again in quadrant IV.
In quadrants II and III cosine has negative values.
In quadrant I (between 0 and pi%2F2 , or if you prefer between0%5Eo and 90%5Eo ),
we have cos%28pi%2F3%29=1%2F2 .
In quadrant IV , 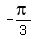-pi%2F3 has a cosine of 1%2F2 too.
Since cosine has a period of 2pi , adding 2pi you get an angle with the same cosine.
So all the angles with a cosine of 1%2F2 can be expressed as
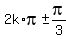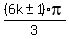2k%2Api+%2B-+pi%2F3=%286k+%2B-+1%29pi%2F3 , for any integer k
If cos%283x%29=1%2F2 , then 3x=%286k+%2B-+1%29pi%2F3 --> x=%286k+%2B-+1%29pi%2F9 .
%286%2A0+-+1%29pi%2F9=-pi%2F9%3C0 and %286%2A3%2B1%29pi%2F9=highlight%2819pi%2F9%3E2pi%29 are outside the interval %22%5B+0+%2C%222pi%22%29%22 .
The solutions in the interval %22%5B+0+%2C%222pi%22%29%22 are
%286%2A0+%2B+1%29pi%2F9=highlight%28pi%2F9%29 , %286%2A1+-+1%29pi%2F9=highlight%285pi%2F9%29 , %286%2A1+%2B+1%29pi%2F9=highlight%287pi%2F9%29 , %286%2A2+-+1%29pi%2F9=highlight%2811pi%2F9%29 , %286%2A2%2B1%29pi%2F9=highlight%2813pi%2F9%29 , %286%2A3+-+1%29pi%2F9=highlight%2817pi%2F9%29 .